
Постройте график функции
 -x2, если |x|≤1
-x2, если |x|≤1
-1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Чтобы построить график функции состоящей из двух подфункций, необходимо построить график каждой подфункции на указанных для них диапазонах и объединить эти графики.
Так как в данном примере диапазоны обозначены неравенствами с
функцией модуля, то сначала решим эти неравенства:
Функция |x| всегда принимает положительные значения, и |x| будет меньше или равен 1, когда -1≤х≤1, т.е. x⊂[-1;1].
Следовательно |x|>1 на всем остальном пространстве, т.е. x⊂(-∞;-1)∪(1;+∞).
Запишем получившуюся функцию:
 -x2, если x⊂[-1;1]
-x2, если x⊂[-1;1]
-1/x, если x⊂(-∞;-1)∪(1;+∞)
Построим по точкам график обоих подфункций в указанных диапазонах:
-x2, если x⊂[-1;1]
| X | -1 | 0 | 1 |
| Y | -1 | -1 |
| X | -5 | -2 | -1 | 1 | 2 | 5 |
| Y | 0,2 | 0,5 | 1 | -1 | -0,5 | -0,2 |
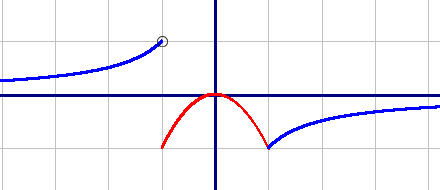 График первой подфункции начерчен красным цветом, график второй подфункции - синим.
График первой подфункции начерчен красным цветом, график второй подфункции - синим.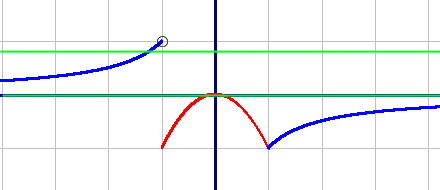 Обратите внимание, что при с=0 прямая касается графика красной подфункции, а при всех остальных значениях - пересекает синюю подфункцию.
Обратите внимание, что при с=0 прямая касается графика красной подфункции, а при всех остальных значениях - пересекает синюю подфункцию.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x|x+3|x|-5x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
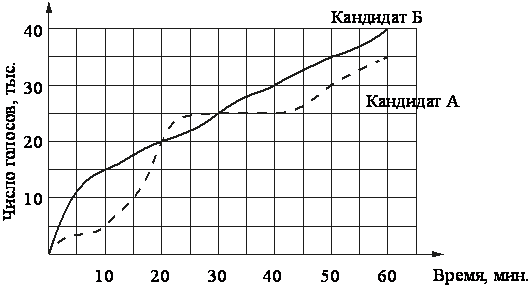 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 40 минут дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 40 минут дебатов?
Постройте график функции 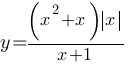 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Постройте график функции y=(x2+6,25)(x-1)/(1-x) и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Комментарии: