
Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Так как функция y=|x2-x-2| содержит
модуль, то данную функцию надо разложить на две функции, в зависимости от значения модуля.
 y=x2-x-2, при x2-x-2≥0
y=x2-x-2, при x2-x-2≥0
y=-(x2-x-2), при x2-x-2<0
Вычислим при каких значениях х функция меняет свой знак, для этого решим неравенство:
x2-x-2≥0
Найдем
корни уравнения x2-x-2=0
D=(-1)2-4*1*(-2)=1+8=9
x1=(-(-1)+3)/(2*1)=4/2=2
x2=(-(-1)-3)/(2*1)=-2/2=-1
 Решением данного неравенства будет диапазон (-∞; -1]∪[2; +∞), и меньше нуля в диапазоне (-1; 2).
Решением данного неравенства будет диапазон (-∞; -1]∪[2; +∞), и меньше нуля в диапазоне (-1; 2).
Значит можем переписать систему:
 y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞)
y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞)
y=-(x2-x-2), при x ∈ (-1; 2)
Построим оба графика по точкам:
1) y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞) (красный график):
| X | -3 | -2 | -1 | 2 | 3 | 4 |
| Y | 10 | 4 | 0 | 0 | 4 | 10 |
| X | -1 | 0 | 1 | 2 |
| Y | 0 | 2 | 2 | 0 |
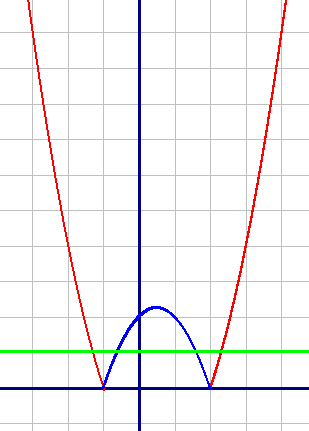 Очевидно, что прямая, параллельная оси абсцисс будет иметь максимум 4 общие точки. Это видно на примере зеленой прямой.
Очевидно, что прямая, параллельная оси абсцисс будет иметь максимум 4 общие точки. Это видно на примере зеленой прямой.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
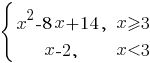
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
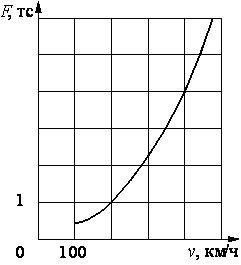 Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, на сколько увеличится подъёмная сила (в тоннах силы) при увеличении скорости с 200 км/ч до 400 км/ч.
Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, на сколько увеличится подъёмная сила (в тоннах силы) при увеличении скорости с 200 км/ч до 400 км/ч.
 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры в первой половине суток. Ответ дайте в градусах Цельсия.
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры в первой половине суток. Ответ дайте в градусах Цельсия.
Постройте график функции y=x2-5|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
 Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Комментарии:
(2022-01-29 19:47:21) : дана функция у=х^-4х,х определи как должна быть расположена прямая параллельная оси абсцисс чтобы иметь с этим графиком ровно две общие точки
(2017-12-06 17:58:19) Администратор: Валентина, для знающего человека, конечно, проще так, как Вы сказали. Мое решение универсальное, чтобы показать, как вообще решаются подобные задачи с модулем.
(2017-12-03 16:10:06) Валентина: Зачем так сложно решать? Построили параболу и отразили ее симметрично относительно оси Ох.