
Постройте график функции y=-2x+4|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 y=-2x+4x-x2, при x≥0
y=-2x+4x-x2, при x≥0
y=-2x+4(-x)-x2, при x<0
 y=2x-x2, при x≥0
y=2x-x2, при x≥0
y=-6x-x2, при x<0
Исследуем каждую подфункцию:
1) y=2x-x2
Это квадратичная функция, следовательно график - парабола. Коэффициент а=-1 (т.е. меньше нуля), следовательно ветви параболы направлены вниз. Найдем точки пересечения графика с осью Х, для этого решим уравнение 2x-x2=0
x(2-x)=0
x1=0
x2=2
2) y=-6x-x2
Это квадратичная функция, следовательно график - парабола. Коэффициент а=-1 (т.е. меньше нуля), следовательно ветви параболы направлены вниз. Найдем точки пересечения графика с осью Х, для этого решим уравнение -6x-x2=0
x(-6-x)=0
x1=0
x2=-6
Построим график для каждой подфункции и объединим их.
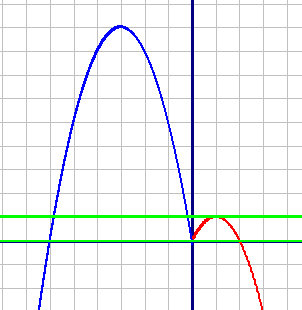 1) y1=2x-x2, при x≥0 (красный график)
1) y1=2x-x2, при x≥0 (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | 1 | 0 | -3 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 0 | 5 | 8 | 9 | 8 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 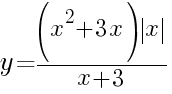
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)  Б)
Б)  В)
В) 
ФОРМУЛЫ
1) y=-(2/x) 2) y=x2-2
3) y=2x
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции
 x2, если |x|≤1
x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Установите соответствие между функциями и их графиками.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | |||
|
А) y=-2x+4 Б) y=2x-4 В) y=2x+4 |
1) 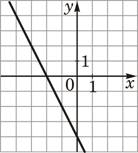 |
2) 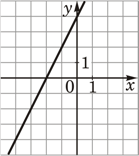 |
3) 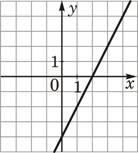 |
4) 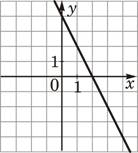 |
Комментарии: