
Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
|x+2|=x+2, при x+2≥0 (т.е. x≥-2)
|x+2|=-(x+2), при х+2<0 (т.е. х<-2)
Тогда вся функция будет выглядеть так:
 x2+3x-4(x+2)+2, при x≥-2
x2+3x-4(x+2)+2, при x≥-2
x2+3x-4(-(x+2))+2, при x<-2
 x2+3x-4x-8+2, при x≥-2
x2+3x-4x-8+2, при x≥-2
x2+3x-4(-x-2)+2, при x<-2
 x2-x-6, при x≥-2
x2-x-6, при x≥-2
x2+3x+4x+8+2, при x<-2
 x2-x-6, при x≥-2
x2-x-6, при x≥-2
x2+7x+10, при x<-2
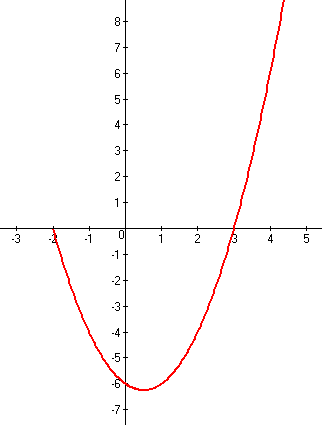 |
График первой функции: y=x2-x-6, при x≥-2 функция квадратичная, следовательно график - парабола. Коэффициент а=1, т.е. больше нуля, следовательно ветви параболы направлены вверх. Найдем точки пересечения графика с осью Х, для это необходимо решить квадратное уравнение x2-x-6=0: D=(-1)2-4*1*(-6)=1+24=25 x1=(-(-1)+5)/(2*1)=6/2=3 x2=(-(-1)-5)/(2*1)=-4/2=-2 Найдем точку пересечения графика с осью Y, для этого вместо х подставим 0: y=02-0-6=-6
|
||||||||||
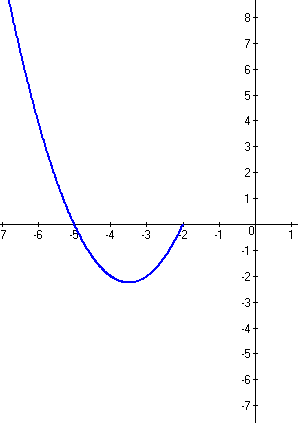 |
График второй функции: y=x2+7x+10, при x<-2 функция квадратичная, следовательно график - парабола. Коэффициент а=1, т.е. больше нуля, следовательно ветви параболы направлены вверх. Найдем точки пересечения графика с осью Х, для это необходимо решить квадратное уравнение x2+7x+10=0: D=72-4*1*10=49-40=9 x1=(-7+3)/(2*1)=-4/2=-2 x2=(-7-3)/(2*1)=-10/2=-5 Найдем точку пересечения графика с осью Y, для этого вместо х подставим 0: y=02+7*0+10=10
|
||||||||||
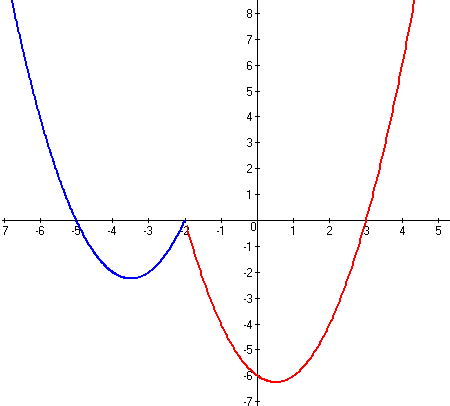 |
Итоговый график функции y=x2+3x-4|x+2|+2 | ||||||||||
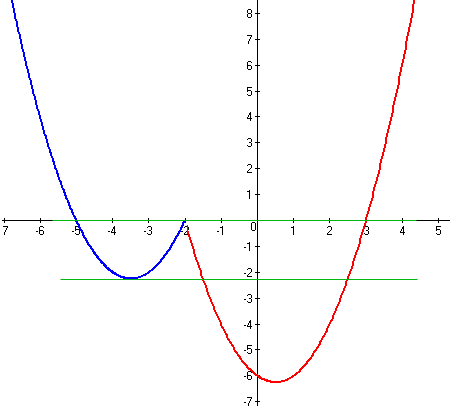 |
Очевидно, что при m=0, функция y=m имеет ровно 3 общие точки с графиком. Но существует еще одно значение m, как показано на рисунке. Данная прямая проходит через вершину второй функции. Координату x0 вершины параболы можно найти по формуле: x0=-b/2a x0=-7/(2*1)=-3,5 Подставим в уравнение и получим, что y0=(-3,5)2+7*(-3,5)+10=12,25-24,5+10=-2,25 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Постройте график функции
y=x|x|+2|x|-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Установите соответствие между графиками функций и формулами, которые их задают. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
| ФОРМУЛЫ | Графики | ||
|
1) y=-x2+7x-14 2) y=x2-7x+14 3) y=x2+7x+14 4) y=-x2-7x-14 |
A)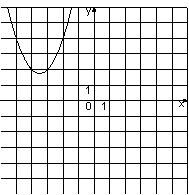
|
Б)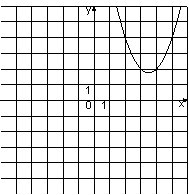
|
В)
|
Постройте график функции y=|x2+5x+6| . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Постройте график функции 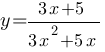 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Комментарии:
(2017-01-14 20:12:51) Администратор: Леночка, отправьте, пожалуйста, заявку на добавление задачи с указанием номера, страницы и раздела (в меню "не нашли задачу?"). Мы обязательно добавим запрошенную задачу.
(2017-01-13 13:11:50) Леночка: Вам ранее задали вопрос по поводу решения подобного задания, вы ответили, что дз не решаете, но это один из возможных вариантов ОГЭ, а решения подобных заданий у Вас нет, поэтому просьба прорешать подобное задание. (постройте график функции y=|4-(x-2)^2|-1 и определите,при каких значениях с,прямая у=с имеет с графиком ровно две общие точки.) п.с. такое задание встречалось уже не раз
(2017-01-13 13:08:50) Леночка: Вам ранее задали вопрос по поводу решения подобного задания, вы ответили, что дз не решаете, но это один из возможных вариантов ОГЭ, а решения подобных заданий у Вас нет, поэтому просьба прорешать подобное задание.
(2017-01-09 21:28:30) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-05 12:46:03) : ispolzuy grafichiskii metod naiti globolnue ekstimumy funksii L=(x1-3)2+(x2-4)2 pri ogranicheniah
(2017-01-04 13:52:18) : постройте график функции y=|4-(x-2)^2|-1 и определите,при каких значениях с,прямая у=с имеет с графиком ровно две общие точки.
(2015-04-10 22:16:26) Администратор: Добавил.
(2015-04-09 11:24:39) Администратор: Хорошо, в скором времени добавлю.
(2015-04-09 11:20:22) : я ожидала , что вы это напишите
(2015-04-09 11:19:08) : я думала, что вы здесь "х1" и "х2", то есть "2" и "3"( в первой функции) нашли через дискриминант.Разве нет?
(2015-04-08 17:01:42) Администратор: Я не написал таблицу с точками, предполагая, что учащиеся это могут сделать самостоятельно, но, видимо, зря. Я добавил таблицы. Спасибо за вопрос.
(2015-04-08 15:51:35) : как вы без расчетов построили график?