
В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии.
Каждый член
геометрической прогрессии можно выразить через первый член.
bn=b1qn-1
Тогда b2=b1q2-1=b1q
По условию:
1) b1+b2=75
b1+b1q=75
b1(1+q)=75
2) b2+b3=150
b1q+b1q2=150
b1(q+q2)=150
b1(q+1)q=150
Подставляем из п. 1)
75q=150 => q=2, тогда b1(1+2)=75 => b1=25
b2=25*2=50
b3=25*22=100
Ответ: b1=25, b2=50, b3=100
Поделитесь решением
Присоединяйтесь к нам...
Последовательность задана условиями a1=5, an+1=an+3. Найдите a10.
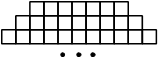 Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 39-й строке?
Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 39-й строке?
В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии.
Выписано несколько последовательных членов арифметической прогрессии:
…; -9; x; -13; -15; …
Найдите x.
Дана арифметическая прогрессия: -3; 1; 5; … . Найдите сумму первых шестидесяти её членов.
Комментарии:
(2015-04-12 14:09:09) Администратор: Екатерина, в п. 1) мы получили b1(1+q)=75, потом мы получили q=2 и подставили в уравнение.
(2015-04-12 12:24:08) Екатерина : Как вы получили b1(1+2)=75?
(2015-04-11 15:55:28) Администратор: Чтобы свести оба уравнения к одним и тем же неизвестным b1 и q.
(2015-04-11 15:53:45) Администратор: По условию задачи: b1+b2=75. b2=b1q. Подставляем в уравнение и получаем b1+b1q=75.
(2015-04-11 15:53:27) : обьясните, зачем мы делали так? b1+b1q=75
(2015-04-11 15:50:58) : b1+b1q=75 почему здесь добавили q?
(2015-04-10 18:37:08) Окс: Спасибо
(2015-04-10 15:40:23) Администратор: Окс, b1+b1q=75, выносим за скобку b1, получается b1(1+q)=75.
(2015-04-10 13:54:06) Окс: Не могу понять как получилось b1(1+q)=75
(2015-03-18 11:37:53) Чапай: Спасибо
(2015-02-13 18:45:58) Администратор: Кристина, в п. 1) мы получили, что b1(1+q)=75, в п. 2) мы получили b1(q+1)q=150 или [b1(1+q)]q=150. Выражение в квадратных скобках равно выражению из п. 1), которое и равно 75. Т.е. b1(1+q) мы заменяем на 75, получаем [75]q=150, т.е. 75q=150.
(2015-02-13 14:15:14) Кристина : Как вы получили выражение 75q=150 ?
(2015-02-13 14:15:10) Кристина : Как вы получили выражение 75q=150 ?