
Постройте график функции y=|x2+5x+6| . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
y=|x2+5x+6|
Данную функцию надо разложить на две функции, в зависимости от значения модуля.
 y=x2+5x+6, при x2+5x+6≥0
y=x2+5x+6, при x2+5x+6≥0
y=-(x2+5x+6), при x2+5x+6<0
Вычислим при каких значениях х функция меняет свой знак, для этого решим неравенство:
x2+5x+6≥0
Найдем
корни уравнения x2+5x+6=0
D=52-4*1*6=25-24=1
x1=(-5+1)/(2*1)=-2
x1=(-5-1)/(2*1)=-3
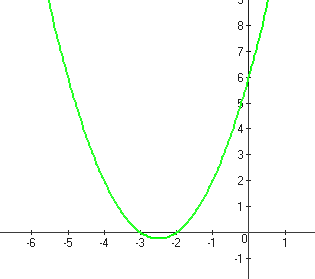
На рисунке представлен график функции y=x2+5x+6, данная функция больше или равна нулю в диапазоне (-∞; -3]∪[-2; +∞), и меньше нуля в диапазоне (-3; -2).
Значит можем переписать систему:
 y=x2+5x+6, при x ∈ (-∞; -3]∪[-2; +∞)
y=x2+5x+6, при x ∈ (-∞; -3]∪[-2; +∞)
y=-(x2+5x+6), при x ∈ (-3; -2)
Тогда график первой функции будет выглядеть так:
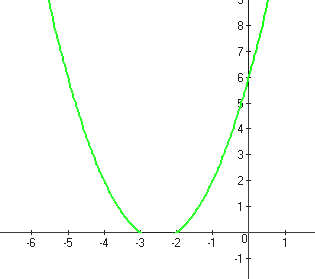
График второй функции выглядит так:

Объединяем графики и получаем:
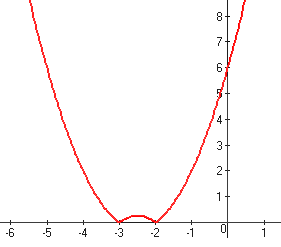
Очевидно, что прямая, параллельная оси абсцисс будет иметь 4 общие точки.
Поделитесь решением
Присоединяйтесь к нам...
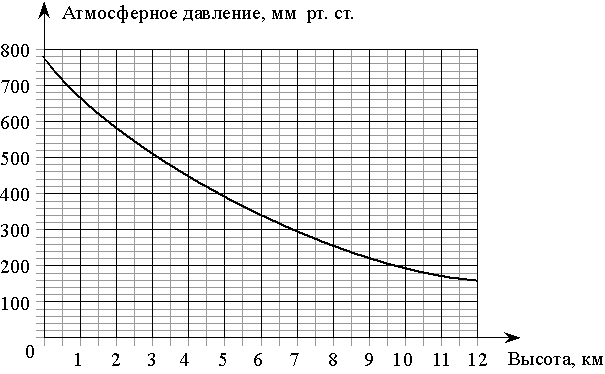 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 360 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 360 миллиметров ртутного столба?
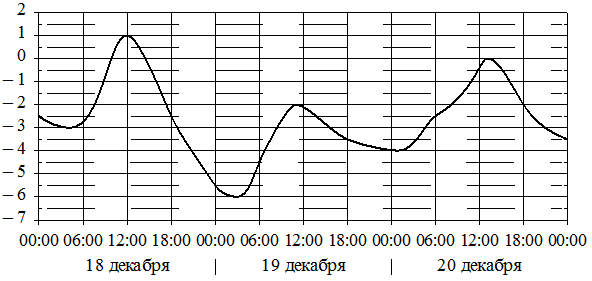 На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 19 декабря. Ответ дайте в градусах Цельсия.
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 19 декабря. Ответ дайте в градусах Цельсия.
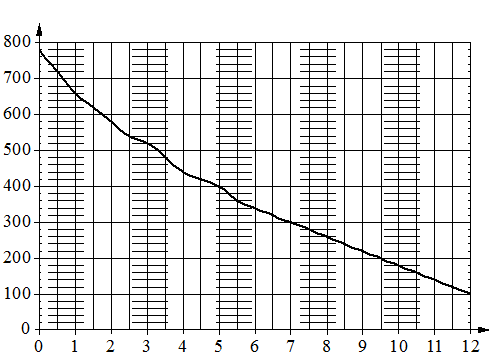 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 11 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 11 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции y=x2-3|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=x2+4 2) y=-2x+4 3) y=-4/x |
А)  |
Б)  |
В)  |
Комментарии:
(2022-09-07 23:21:16) Ирина: Постройте график функции y=x|x|-|x|-3x Определите, при каких значениях m прямая y m= имеет с графиком ровно две общие точки.
(2020-12-26 23:34:01) Аня: Найдите нули функции f(х) = x^2-5x+6/x-3
(2017-08-13 22:23:45) Администратор: Саша, я немного структурировал решение, надеюсь стало понятно.
(2017-08-04 13:00:43) саша: почему вы нижнию часть перевернули вверх дном.
(2015-12-13 18:59:18) Администратор: Илья, конечно, желания что-то подпортить нет ))) Этот шрифт выбран, так как подходит по тематике сайта. Я подумаю над возможностью выбирать шрифт, спасибо за идею.
(2015-12-13 18:17:27) Илья.: Спасибо авторам. Спасибо большое. Но видимо есть желание подпортить чем то дело. Усложнить пользование сайтом. Почему использован ручной шрифт. Он очень нечитабельный. Мучение одно читать его. Почему б ыне использовать хотя бы тот же ариал.
(2015-04-10 18:15:05) Администратор: Светлана, так и есть: у=х+5х+6 и у=-(х+5х+6)=у=-х-5х-6. Только нужно указать: на каком диапазоне у=х+5х+6, а на каком у=-х-5х-6.
(2015-04-10 16:24:00) светлана: здесь разве не должно быть у=х+5х+6 и у=-х-5х-6?
(2015-04-08 11:33:01) Администратор: Конечно любой график можно просто построить по точкам, но если не проанализировать функцию, то заранее не будет понятно, как приблизительно будет выглядеть график. Поэтому придется вычислять Y для очень многих X. Для большинства функций эта задача очень трудоемкая. А вычислив ключевые точки функции нам остается вычислить только несколько уточняющих точек для построения.
(2015-04-08 11:27:07) : А нельзя было найти значения "у" через " х" и затем начертить по нему график?
(2015-04-08 11:27:06) : А нельзя было найти значения "у" через " х" и затем начертить по нему график?
(2015-03-03 16:55:30) Администратор: x<-3 значит, что х может быть равен -4, -5, -6 и т.д. -10000000000, и дальше до минус бесконечности.
(2015-03-03 15:20:23) : нет, почему именно от минус бесконечности диапазон ?
(2015-03-02 18:02:54) Администратор: А все, что на графике ниже оси Х, убирается (стирается).
(2015-03-02 18:01:59) Администратор: Когда мы раскрыли модуль, то определили, что первая подфункция должна быть больше или равна нулю. Любая функция больше нуля, когда ее график расположен выше оси Х. График нашей первой подфункции находится выше оси Х, когда x<-3 и когда x>-2. Поэтому получились такие диапазоны.
(2015-03-02 17:24:59) : И ПОЧЕМУ У ГРАФИКА ПЕРВОЙ ФУНКЦИИ ТАК ВЫРЕЗАНО ?
(2015-03-02 17:17:54) : равна нулю в диапазоне (-∞; -3]∪[-2; ПОЧЕМУ ЗДЕСЬ ТАК?
(2015-03-01 18:42:29) Администратор: Саша, просто по графику. Если провести, например, прямую y=0,1 (она будет параллельна оси Х), то она пересечет график 4 раза. Саша, наложите линейку (параллельно оси Х) на график в разных местах и увидите количество точек пересечения.
(2015-03-01 17:35:04) Саша: Как вы определили что будет 4
(2015-02-25 18:34:15) Администратор: Саша, Вы имеете в виду, как найти координаты этих 4-х точек, или как мы определили, что точек будет 4?
(2015-02-25 18:21:26) Саша: Как понять какие 4 точки
(2014-09-27 10:19:43) Валерий: Супер, спасибо!!!