Задача №3 из 42 |
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
Условие задачи очень похоже на арифметическую прогрессию, где:
a1=4200
d=1300
А найти надо S11.
Воспользуемся формулой суммы арифметической прогрессии.
Для практики, найдем сумму сначала по первой формуле, а потом по второй:
1) Для первой формулы надо найти a11:
a11=a1+(n-1)d=4200+(11-1)1300=4200+10*1300=17200
S11 = n*(a1+a11)/2 = 11*(4200+17200)/2=11*10700 = 117700
2) Для второй формулы ничего дополнительно искать не надо:
S11 = n*(2a1+(n-1)d)/2 = 11*(2*4200+(11-1)1300)/2 = 11*(8400+10*1300)/2 = 11*(8400+10*1300)/2 = 11*21400/2 = 11*10700 = 117700 руб.
Можно заменить, что вторая формула - это первая формула, только расписанная более подробно.
Ответ: 117700
Поделитесь решением
Присоединяйтесь к нам...
Хозяйка к празднику купила морс, мороженое, крабовые палочки и рыбу. Мороженое стоило дороже крабовых палочек, но дешевле рыбы, морс стоил дешевле мороженого. Выберите утверждения, которые верны при указанных условиях.
1) Морс стоил дешевле рыбы.
2) За морс заплатили больше, чем за мороженое.
3) Рыба — самая дорогая из покупок.
4) Среди указанных четырёх покупок есть три, стоимость которых одинакова.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Найдите корень уравнения 
Найдите корень уравнения 
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x-1)2(x-4)<0 | 1) (-∞; 1)∪(4; +∞) |
Б)  |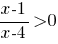
2) (1; 4)∪(4; +∞) |
| В) (x-1)(x-4)<0 | 3) (-∞; 1)∪(1; 4) |
Г)  |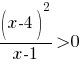
4) (1; 4) |
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: