Задача №31 из 42 |
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым — 12 кусков, а если по зелёным — 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Если палку распилить в одном месте, то получится 2 куска.
Если в двух местах - 3 куска.
Если в трех - 4 куска и т.д.
Т.е. кусков получается на 1 больше, чем мест распила.
Следовательно, если получается 9 кусков при распиле по красным линиям, то самих линий 8. Аналогично вычисляем, что желтых линий 11, а зеленых - 7.
Всего линий 8+11+7=26.
Поэтому, сделав 26 распилов по всем линиям, мы получим 27 кусков.
Ответ: 27
Поделитесь решением
Присоединяйтесь к нам...
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
А)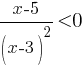 
|
1) 
|
Б)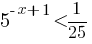 
|
2) 
|
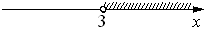
| В) (x-3)(x-5)>0 |
3) 
|
| Г) log2(x-3)<1 |
4) 
|
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x-1)2(x-4)<0 | 1) (-∞; 1)∪(4; +∞) |
Б)  |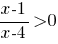
2) (1; 4)∪(4; +∞) |
| В) (x-1)(x-4)<0 | 3) (-∞; 1)∪(1; 4) |
Г)  |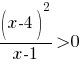
4) (1; 4) |
На координатной прямой отмечены точки A, B, C и D.
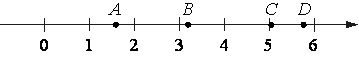
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) √11+√3 |
| B | 2) √11*√3 |
| C | 3) √11-√3 |
| D | 4) (√3)3-2 |
Найдите корень уравнения √
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: