
Задача №8 из 42 |
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Рассмотрим каждое утверждение:
1) Если Шарик не лает, значит, по забору идёт кошка. Это утверждение неверно, так как противоречит условию, что "Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает".
2) Если Шарик молчит, значит, кошка по забору не идёт. Это утверждение верно, так как полностью соответствует условию.
3) Если по забору идёт чёрная кошка, Шарик не лает. Это утверждение неверно, так как Шарик лает не зависимо от цвета кошли.
4) Если по забору пойдёт белая кошка, Шарик будет лаять. Это утверждение верно, так как Шарик будет лаять не зависимо от цвета кошли.
Ответ: 24
Поделитесь решением
Присоединяйтесь к нам...
Некоторые учащиеся 11-х классов школы ходили в октябре на спектакль «Вишнёвый сад». В декабре некоторые одиннадцатиклассники пойдут
на постановку по пьесе «Три сестры», причём среди них не будет тех, кто ходил в октябре на спектакль «Вишнёвый сад».
Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из одиннадцатиклассников пойдёт на постановку по пьесе «Три сестры».
1) Нет ни одного одиннадцатиклассника, который ходил на спектакль «Вишнёвый сад» и пойдёт на постановку по пьесе «Три сестры».
2) Каждый учащийся 11-х классов, который не был на спектакле «Вишнёвый сад», пойдёт на постановку по пьесе «Три сестры».
3) Среди учащихся 11-х классов этой школы, которые не пойдут на постановку по пьесе «Три сестры», есть хотя бы один, который ходил на спектакль «Вишнёвый сад».
4) Найдётся одиннадцатиклассник, который не ходил на спектакль «Вишнёвый сад» и не пойдёт на постановку по пьесе «Три сестры».
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
A) 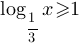
|
1) 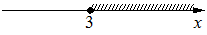
|
Б) 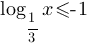
|
2) 
|
В) 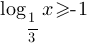
|
3) 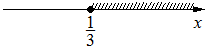
|
Г) 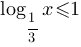
|
4) 
|
Найдите корень уравнения √
Решите уравнение x2=-2x+24.
Если уравнение имеет более одного корня, в ответе укажите больший из них.
Комментарии: