Задача №12 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
A)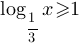 
|
1) 
|
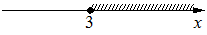
Б)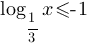 
|
2) 
|
В)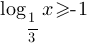 
|
3) 
|
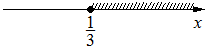
Г)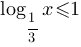 
|
4) 
|
Решим каждое неравенство:
A)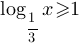
По
второму свойству логарифмов, в правой части неравенства преоразуем единицу в логарифм:
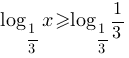
Основание логарифмоы = 1/3, т.е. меньше единицы, следовательно по
теореме для решения логарифмических неравенств:
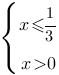
- подходит вариант 4)
Для неравенства Г)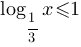 можно сразу определить ответ - вариант 3), так как неравенства отличаются только знаком.
Б)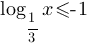
По
второму свойству логарифмов, в правой части неравенства преоразуем единицу в логарифм:
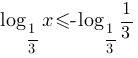
При помощи 6-го свойства, внесем -1 в логарифм.
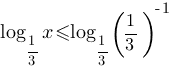
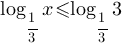
Основание логарифмоы = 1/3, т.е. меньше единицы, следовательно по
теореме для решения логарифмических неравенств:
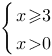
- подходит вариант 1)
Для неравенства В)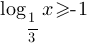 можно сразу определить ответ - вариант 2), так как неравенства отличаются только знаком.
Ответ:
| A) | Б) | В) | Г) |
| 4) | 1) | 2) | 3) |
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения √
Каждому из четырёх неравенств в левом столбце соответствует одно
из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| A) 2-x+1<0,5 | 1) (4;+∞) |
| Б) (x-5)2/(x-4)<0 | 2) (2;4) |
| В) log4x>1 | 3) (2;+∞) |
| Г) (x-4)(x-2)<0 | 4) (-∞;4) |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
А)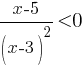 
|
1) 
|
Б)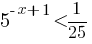 
|
2) 
|
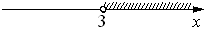
| В) (x-3)(x-5)>0 |
3) 
|
| Г) log2(x-3)<1 |
4) 
|
Маша младше Алисы на год, но старше Кати на два года. Выберите утверждения, которые верны при указанных условиях.
1) Любая девочка, помимо указанных, которая старше Кати, также старше Маши.
2) Среди указанных девочек нет никого младше Кати.
3) Любая девочка, помимо указанных, которая старше Маши, также старше Кати.
4) Алиса и Катя одного возраста.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
На координатной прямой отмечены точки A, B, C и D.
Число m равно √
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: