
При каких значениях р вершины парабол у=х2-2рх-1 и у=-х2+4рх+р расположены по разные стороны от оси х?
Рассмотрим предложенные
квадратные уравнения:
В первом уравнении а=1, т.е. больше 0, значит ветви этой параболы смотрят вверх;
во-втором уравнении а=-1, т.е. меньше 0, значит ветви смотрят вниз.
Возможны два варианта:
1) Оба графика не пересекают ось х как на рисунке 1.
2) Оба графика пересекают ось х дважды, как на рисунке 2.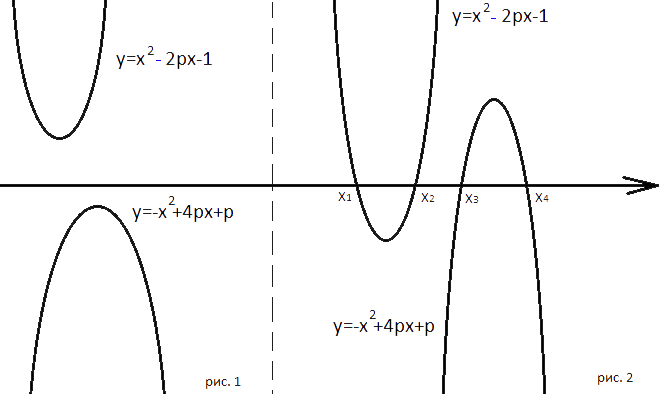 Рассмотрим каждый вариант:
Рассмотрим каждый вариант:
1) Чтобы графики функций не пересекали ось х, уравнения функций не должны иметь
корней. Для
квадратного уравнения это означает, что
дискриминант меньше нуля:
D1=(-2p)2-4*1*(-1)=4p2+4<0
4p2+4<0
4p2<-4
p2<-1, это невозможно (квадрат числа всегда больше либо равен нулю).
Значит вариант первый отпадает (D2 можно даже не вычислять).
Рассмотрим второй вариант, для второго варианта
дискриминант должен быть строго больше нуля:
D1=(-2p)-4*1*(-1)=4p2+4>0 => p2>-1, это неравенство выполняется для любого p
D2=(4p)2-4*(-1)*p=16p2+4p>0, решим это неравенство.
16p2+4p>0
4(4p2+p)>0
4p2+p>0
p(4p+1)>0
Чтобы это неравенство выполнялось должно быть:
1) или p>0 и 4p+1>0
2) или p<0 и 4p+1<0
1) p>0 и p>-1/4 => p>0
2) p<0 и p<-1/4 => p<-1/4
Ответ: p=(-∞;-1/4)∪(0;+∞)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
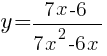
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Найдите значение выражения (x-5)2-x(10+x) при x=-1/20.
Найдите значение выражения 2-7*2-8/2-9.
1) 1/64
2) -1/64
3) -64
4) 64
Решите уравнение (x-3)(x-4)(x-5)=(x-2)(x-4)(x-5).
Упростите выражение 
Комментарии:
(2016-11-06 18:08:30) Администратор: Людмила, в первом варианте ни при каких P дискриминант не будет меньше нуля. Т.е. при любых P у первой функции будут корни, т.е. функция будет пересекать ось OX. Следовательно первый вариант не возможен.
(2016-11-06 17:52:05) Людмила: Как раз первый вариант и подходит, так как первая парабола расположена выше оси ОХ (D1<0), то вторая парабола должна быть расположена ниже оси ОХ (D2<0)и ответ будет р=(-0.25;0)
(2015-05-23 14:00:30) Администратор: Добавлю, но не сейчас.
(2015-05-23 13:57:32) : А вы не хотели бы добавить второй способ, если не сложно?)
(2015-02-09 09:31:51) Администратор: Саша, можно и через координаты вершин парабол, но, по-моему, трудозатраты такие же.
(2015-02-08 17:41:26) Администратор: Саша, можно и через координаты вершин парабол, но, по-моему, трудозатраты такие же.
(2015-02-08 17:38:04) Саша: А не легче ли было решать через вершины порабол??????????????