
В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что спортсмен из Швеции будет стартовать последним.
Вероятность любого события равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
В данной задаче интересующее нас событие - старт спортсмена из Швеции последним.
Старт последним одного из семи российских спортсменов - неблагоприятный исход
Старт последним швейцарского спортсмена - благоприятный исход
Старт последним одного из двух норвежских спортсменов - неблагоприятный исход.
Полная группа исходов (благоприятных и неблагоприятных) = 7+1+2=10.
P=1/10=0,1 или 10% (можно указывать ответ в любом виде).
Ответ: P=0,1
Поделитесь решением
Присоединяйтесь к нам...
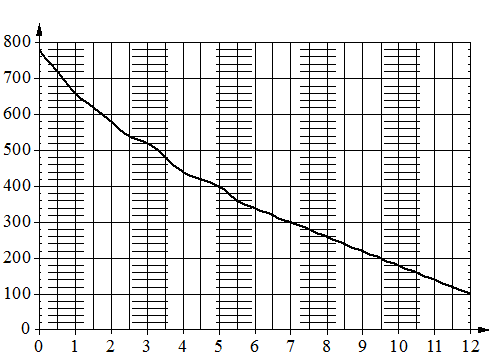 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 780 миллиметрам ртутного столба. Ответ дайте в километрах.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 780 миллиметрам ртутного столба. Ответ дайте в километрах.
В соревнованиях по художественной гимнастике участвуют: три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
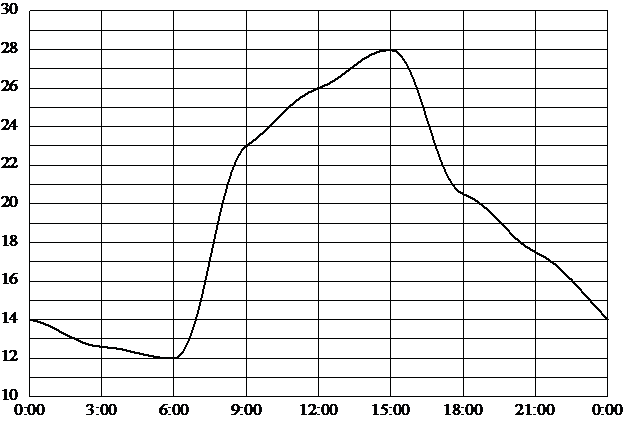 На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов в первой половине суток температура превышала 23°C?
На рисунке показано, как изменялась температура на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов в первой половине суток температура превышала 23°C?
Из 500 семян фасоли в среднем 125 не всходят. Какова вероятность того, что случайно выбранное семя фасоли взойдет?
Какая из следующих круговых диаграмм показывает распределение оценок по контрольной работе по математике в 8 классе, если пятерок в классе примерно 17% всех оценок, четверок – примерно 43%, троек – примерно 28% и двоек – примерно 12%?
1)  2)
2)  3)
3)  4)
4) 
Комментарии: