Решите уравнение (x-3)(x-4)(x-5)=(x-2)(x-4)(x-5).
(x-3)(x-4)(x-5)=(x-2)(x-4)(x-5)
(x-3)(x-4)(x-5)-(x-2)(x-4)(x-5)=0
Выносим за скобки (x-4)(x-5):
(x-4)(x-5)(x-3-(x-2))=0
(x-4)(x-5)(x-3-x+2)=0
(x-4)(x-5)(-1)=0 |:(-1)
(x-4)(x-5)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x-4=0 => x1=4
2) x-5=0 => x2=5
Ответ: x1=4, x2=5.
Поделитесь решением
Присоединяйтесь к нам...
Квадратный трёхчлен разложен на множители: x2-2x-3=(x+1)(x-a). Найдите a.
Уравнение x2+px+q=0 имеет корни -5 и 2. Найдите q.
Магазин закупил на складе футболки и стал продавать их по цене на 60% больше закупочной. В конце года цена была снижена на 50%. Какая цена меньше: та, по которой магазин закупил футболки, или их цена в конце года – и на сколько процентов?
Постройте график функции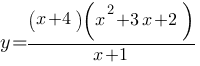 
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Упростите выражение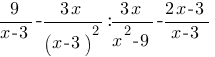 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: