
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А) 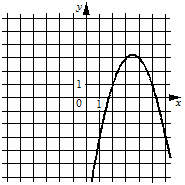 Б)
Б) 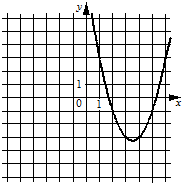 В)
В) 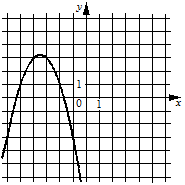
ФОРМУЛЫ
1) y=x2-7x+9
2) y=-x2-7x-9
3) y=-x2+7x-9
В таблице под каждой буквой укажите соответствующий номер.
Посмотрим на графики, на двух графиках ветви парабол направлены вниз, а на одном вверх.
Ветви направлены вверх, когда коэффициент при x2 больше нуля.
Только формула 1) имеет положительных коэффициент, следовательно, она соответствует графику Б).
Идем дальше:
График А) пересекает ось Х в положительной ее части (т.е. имеет положительные корни), а график В) - в отрицательной (т.е. имеет отрицательные корни). Поэтому найдем корни одного из уравнений (например для 3) через
дискриминант.
y=-x2+7x-9
D=72-4*(-1)*(-9)=49-36=13
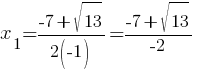
Нам надо выяснить, положительное это число или отрицательное:
√13≈3,6
Следовательно, -7+3,6=-3,4 - отрицательное число.
-3,4/(-2)=1,7 - положительное число.
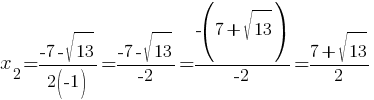
Очевидно, что x2 тоже положительный.
Т.е. формула 3) соответствует графику А).
Методом исключения: формула 2) соответствует графику В).
Ответ:
| Графики | А) | Б) | В) |
| Формулы | 3) | 1) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b..
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) k<0, b<0 2) k>0, b<0 3) k<0, b>0 4) k>0, b>0 |
А)  |
Б)  |
В)  |
Постройте график функции
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Установите соответствие между функциями и их графиками.
| ФУНКЦИИ | ГРАФИКИ | |
|
А) y=-2x2+2x+3 Б) y=-3/x В) y=(5/3)x-1 |
1) 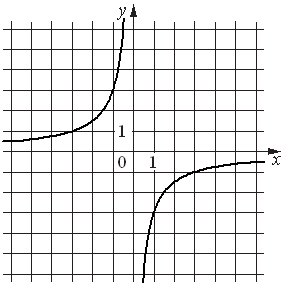 |
2) 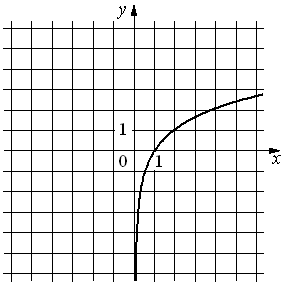 |
3) 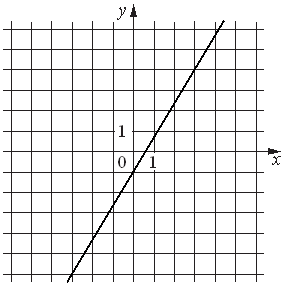 |
4) 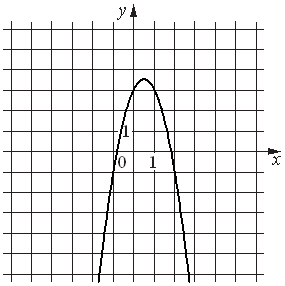 |
На рисунке изображены графики функций вида y=ax2+c. Установите соответствие между графиками и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | |||
|
1) a>0, c<0 2) a<0, c>0 3) a>0, c>0 4) a<0, c<0 |
А) 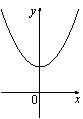 |
Б) 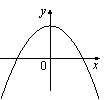 |
В) 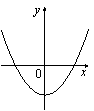 |
Г) 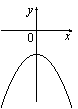 |
Комментарии: