Постройте график функции
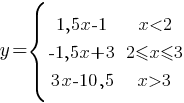
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Построим графики всех трех подфункций на определенным им диапазонах.
Первая подфункция:
y1=1,5x-1, при x<2.
График функции представляет из себя прямую.
Вторая подфункция:
y2=-1,5x+3, при 2≤x≤3 - прямая.
Третья подфункция:
y3=3x-10,5, при x>3 - тоже прямая.
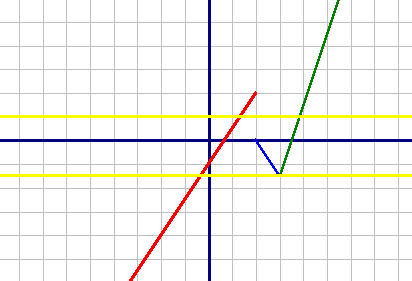Построим все три графика по точкам:
y1=1,5x-1, при x<2 (красный).
| X | 0 | 1 | 2 |
| Y | -1 | 0,5 | 2 |
| X | 2 | 3 |
| Y | 0 | -1,5 |
| X | 3 | 4 | 5 |
| Y | -1,5 | 1,5 | 4,5 |
Поделитесь решением
Присоединяйтесь к нам...
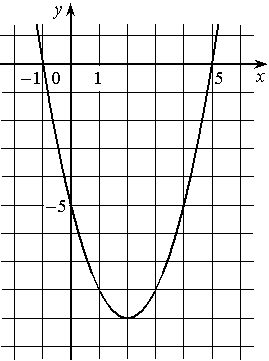На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-3 2) y=x-3 3) y=-3x 4) y=3x |
А)  |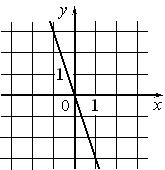
Б)  |
В)  |
Постройте график функции y=x2+14x-3|x+8|+48 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A)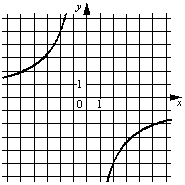 
Б) 
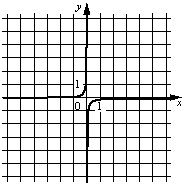В)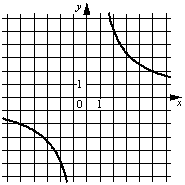 
ФОРМУЛЫ
1) y=-10/x
2) y=-1/(10x)
3) y=10/x
В таблице под каждой буквой укажите соответствующий номер.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: