Постройте график функции
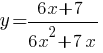
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Отметим Область допустимых Значений (ОДЗ).
На ноль делить нельзя, следовательно:
6x2+7x≠0
x(6x+7)≠0
x1≠0
6x+7≠0
6x≠-7
x2≠-7/6
Т.е. x не может равняться 0 и -7/6.
Теперь упростим нашу функцию:
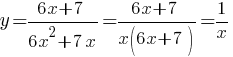
Получили простую гиперболическую функцию, значит график - гипербола.
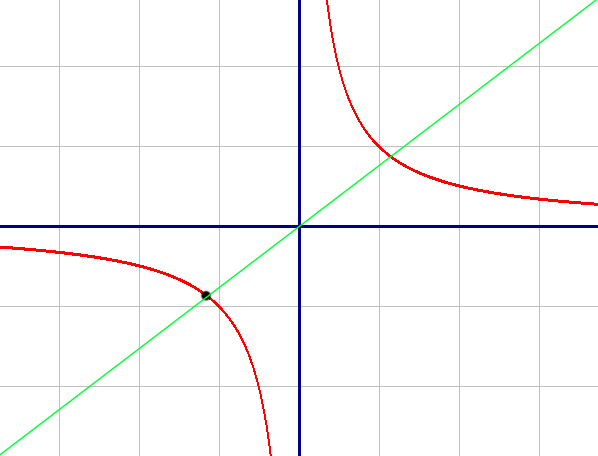Построим график по точкам:
| X | -3 | -2 | -1 | 1 | 2 | 3 |
| Y | -1/3 | -1/2 | -1 | 1 | 1/2 | 1/3 |
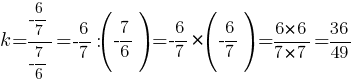
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 
Определите, при каких значениях m прямая y=m не имеет с графиком
ни одной общей точки.
На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки
на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Мурманске в данный период. Ответ дайте в миллиметрах.
Постройте график функции 
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
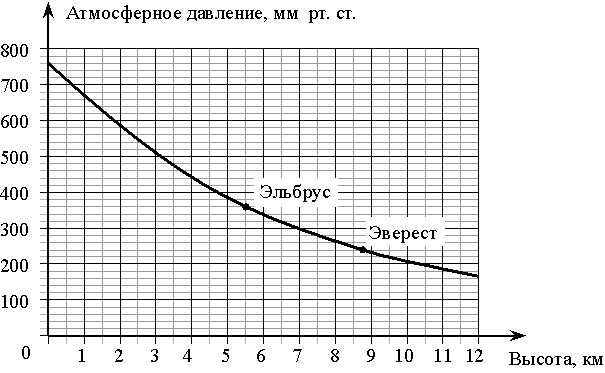На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по
вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления в четверг в 6 часов утра. Ответ дайте в мм рт. ст.
Постройте график функции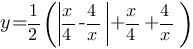 
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: