
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ79 –ł–∑ 287 |
–Ě–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ—č –≥—Ä–į—Ą–ł–ļ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –≤–ł–ī–į y=kx+b. –£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É –≥—Ä–į—Ą–ł–ļ–į–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ł –∑–Ĺ–į–ļ–į–ľ–ł –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ĺ–≤ k –ł b.
| –ö–ě–≠–§–§–ė–¶–ė–ē–Ě–Ę–ę | –ď–†–ź–§–ė–ö–ė | ||
|
1) k>0, b<0 2) k<0, b<0 3) k<0, b>0 4) k>0, b>0 |
–ź)  |
–Ď)  |
–í)  |
–ē—Ā–Ľ–ł –Ņ—Ä—Ź–ľ–į—Ź —Ā–Ľ–Ķ–≤–į –Ĺ–į–Ņ—Ä–į–≤–ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā, —ā–ĺ k>0 (–ļ–į–ļ –Ĺ–į –≥—Ä–į—Ą–ł–ļ–į—Ö –ź) –ł –í)), –ł –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā, –Ķ—Ā–Ľ–ł –Ņ—Ä—Ź–ľ–į—Ź —Ā–Ľ–Ķ–≤–į –Ĺ–į–Ņ—Ä–į–≤–ĺ —É–Ī—č–≤–į–Ķ—ā, —ā–ĺ k<0 (–ļ–į–ļ –Ĺ–į –≥—Ä–į—Ą–ł–ļ–Ķ –Ď).
–£–∑–Ĺ–į—ā—Ć –∑–Ĺ–į–ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į b, –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł—Ä–į–≤–Ĺ—Ź–≤ —Ö –ļ –Ĺ—É–Ľ—é. –ü–ĺ–Ľ—É—á–ł–ľ: y=k*0+b=b.
–ü–ĺ—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ĺ–į –≥—Ä–į—Ą–ł–ļ –ł —É–∑–Ĺ–į–Ķ–ľ b –Ī–ĺ–Ľ—Ć—ą–Ķ –Ĺ—É–Ľ—Ź –ł–Ľ–ł –ľ–Ķ–Ĺ—Ć—ą–Ķ. –Ę.–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā b - —ć—ā–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į "y" —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ –ł –ĺ—Ā–ł y. –Ę–ĺ–≥–ī–į:
–Ē–Ľ—Ź –≥—Ä–į—Ą–ł–ļ–į –ź): k>0, b>0 - –≤–į—Ä–ł–į–Ĺ—ā 4)
–Ē–Ľ—Ź –≥—Ä–į—Ą–ł–ļ–į –Ď): k<0, b>0 - –≤–į—Ä–ł–į–Ĺ—ā 3)
–Ē–Ľ—Ź –≥—Ä–į—Ą–ł–ļ–į –í): k>0, b<0 - –≤–į—Ä–ł–į–Ĺ—ā 1)
–ě—ā–≤–Ķ—ā: –ź) - 4), –Ď) - 3), –í) - 1)
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
–ü–ĺ—Ā—ā—Ä–ĺ–Ļ—ā–Ķ –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł
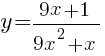
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ, –Ņ—Ä–ł –ļ–į–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö k –Ņ—Ä—Ź–ľ–į—Ź y=kx –ł–ľ–Ķ–Ķ—ā —Ā –≥—Ä–į—Ą–ł–ļ–ĺ–ľ —Ä–ĺ–≤–Ĺ–ĺ –ĺ–ī–Ĺ—É –ĺ–Ī—Č—É—é —ā–ĺ—á–ļ—É.
–ü–ĺ—Ā—ā—Ä–ĺ–Ļ—ā–Ķ –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł

–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ, –Ņ—Ä–ł –ļ–į–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö m –Ņ—Ä—Ź–ľ–į—Ź y=m –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā —Ā –≥—Ä–į—Ą–ł–ļ–ĺ–ľ –Ĺ–ł –ĺ–ī–Ĺ–ĺ–Ļ –ĺ–Ī—Č–Ķ–Ļ —ā–ĺ—á–ļ–ł.
–£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł –ł –ł—Ö –≥—Ä–į—Ą–ł–ļ–į–ľ–ł.
–§–£–Ě–ö–¶–ė–ė
–ź) 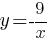 –Ď)
–Ď) 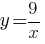 –í)
–í) 
–ď–†–ź–§–ė–ö–ė
1) 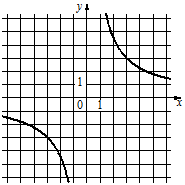 2)
2) 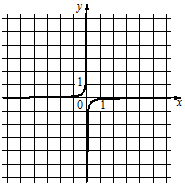 3)
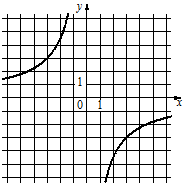
3) 
–í —ā–į–Ī–Ľ–ł—Ü–Ķ –Ņ–ĺ–ī –ļ–į–∂–ī–ĺ–Ļ –Ī—É–ļ–≤–ĺ–Ļ —É–ļ–į–∂–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ –Ĺ–ĺ–ľ–Ķ—Ä.
–ü–ĺ—Ā—ā—Ä–ĺ–Ļ—ā–Ķ –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł
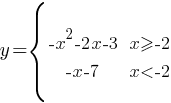
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ, –Ņ—Ä–ł –ļ–į–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö m –Ņ—Ä—Ź–ľ–į—Ź y=m –ł–ľ–Ķ–Ķ—ā —Ā –≥—Ä–į—Ą–ł–ļ–ĺ–ľ —Ä–ĺ–≤–Ĺ–ĺ –ī–≤–Ķ –ĺ–Ī—Č–ł–Ķ —ā–ĺ—á–ļ–ł.
–ü–ĺ—Ā—ā—Ä–ĺ–Ļ—ā–Ķ –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł
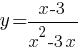
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ, –Ņ—Ä–ł –ļ–į–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö k –Ņ—Ä—Ź–ľ–į—Ź y=kx –ł–ľ–Ķ–Ķ—ā —Ā –≥—Ä–į—Ą–ł–ļ–ĺ–ľ —Ä–ĺ–≤–Ĺ–ĺ –ĺ–ī–Ĺ—É –ĺ–Ī—Č—É—é —ā–ĺ—á–ļ—É.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: