Постройте график функции
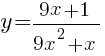
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Отметим Область допустимых Значений (ОДЗ).
На ноль делить нельзя, следовательно:
9x2+x≠0
x(9x+1)≠0
x1≠0
9x+1≠0
9x≠-1
x2≠-1/9
Т.е. x не может равняться 0 и -1/9.
Теперь упростим нашу функцию:
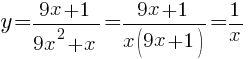
Получили простую гиперболическую функцию, значит график - гипербола.
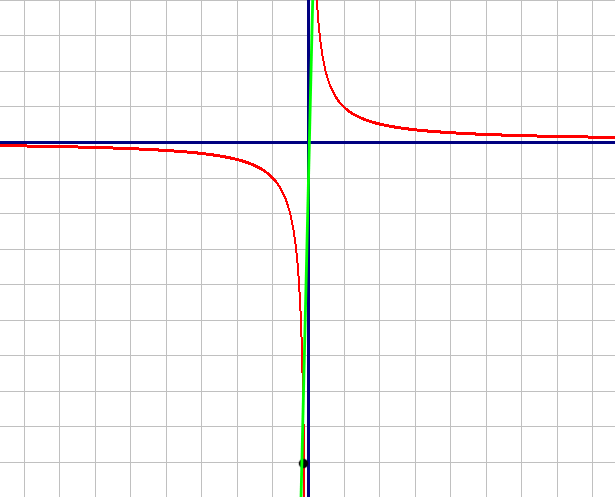Построим график по точкам:
| X | -3 | -2 | -1 | 1 | 2 | 3 |
| Y | -1/3 | -1/2 | -1 | 1 | 1/2 | 1/3 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции
y=x|x|+2|x|-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
-x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Известно, что графики функций y=x2+p и y=2x-5 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x)<0 при -1<x<5
2) Функция возрастает на промежутке [2; +∞)
3) Наименьшее значение функции равно -5
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: