
Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?
Введем обозначения:
S - площадь забора
x - производительность Игоря, т.е. с какой скоростью Игорь красит забор, пусть измеряется в м2/час. Иными словами, Игорь может покрасить х квадратных метров в час.
y - производительность Паши
z - производительность Володи
Составим уравнения:
20(x+y)=S - уравнение означает (из условия), что при производительности x+y забор площадью S будет покрашен за 20 часов.
24(y+z)=S
30(x+z)=S
Преобразуем эти уравнения:
x+y=S/20
y+z=S/24
x+z=S/30
Сложим эти уравнения:
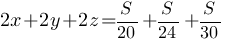
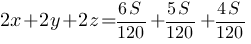
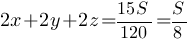
8(2x+2y+2z)=S
8*2(x+y+z)=S
16(x+y+z)=S, расшифруем уравнение:
При производительности x+y+z (т.е. когда работают все три мальчика) забор площадью S будет покрашен за 16 часов.
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
На каком рисунке изображено множество решений системы неравенств
 х+4≥-4,5
х+4≥-4,5
х+4≤0?
1) 
2) 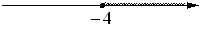
3) 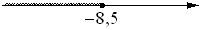
4) 
Укажите неравенство, которое не имеет решений.
1) x2-64≤0
2) x2+64≥0
3) x2-64≥0
4) x2+64≤0
Решите систему уравнений
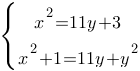
Решите уравнение 1/x2+2/x-3=0.
Комментарии: