Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Первое: 6 целых и 2/3 ч. - это 6 часов 40 минут.
Второе: если лодка идет по течению реки, то ее скорость складывается со скоростью реки, а если против течения, то вычитается.
Обозначим:
скорость реки - v
Время лодки в пути по течению - t1
Время лодки в пути против течения - t2
Движение лодки по течению (1):
24=(10+v)t1
Движение лодки против течения (2):
24=(10-v)t2
При этом, время в пути составило t1+t2, и равно это 6 часов 40 минут минус 1 час 40 мин (на стоянку) и равно это 5 часов (3).
(1) t1=24/(10+v)
(2) t2=24/(10-v)
Подставляем в (3):
24/(10+v)+24/(10-v)=5
Приводим к общему знаменателю:
(24(10-v)+24(10+v))/((10+v)(10-v))=5
480/(102-v2)=5
480=5*(100-v2)
480=500-5v2
5v2=500-480
5v2=20
v2=4
v=2
Ответ: скорость реки равна 2 км/ч
Поделитесь решением
Присоединяйтесь к нам...
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Решите систему уравнений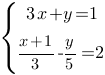 
Решите неравенство:
14/(x2+2x-15)≤0
.
Решите уравнение x2-144=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Решите уравнение (x-1)4-2(x-1)2-3=0.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-24 07:04:22) Администратор: Sabit, шесть целых и две трети часа
(2014-05-23 19:20:33) Sabit : а что такое "все путишествие заняло 6&frac23"?