Школа приобрела стол, доску, магнитофон и принтер. Известно, что принтер дороже магнитофона, а доска дешевле магнитофона и дешевле стола. Выберите утверждения, которые верны при указанных условиях.
1) Магнитофон дешевле доски.
2) Принтер дороже доски.
3) Доска — самая дешёвая из покупок.
4) Принтер и доска стоят одинаково.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Другие задачи из этого раздела

Задача №DA4EF3

Найдите корень уравнения 4^x-6=64.

Задача №757449

Решите уравнение x²=-2x+24.
Если уравнение имеет более одного корня, в ответе укажите больший из них.

Задача №58DA4C

Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА	РЕШЕНИЯ
A)	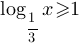1)
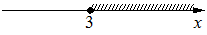
Б)	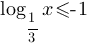2)
В)	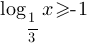3)
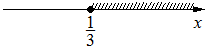
Г)	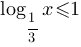4)

Задача №694B19

На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым — 12 кусков, а если по зелёным — 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

Задача №402FF2

Маша младше Алисы на год, но старше Кати на два года. Выберите утверждения, которые верны при указанных условиях.
1) Любая девочка, помимо указанных, которая старше Кати, также старше Маши.
2) Среди указанных девочек нет никого младше Кати.
3) Любая девочка, помимо указанных, которая старше Маши, также старше Кати.
4) Алиса и Катя одного возраста.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.