Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)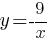 
Б) 
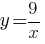В) 
ГРАФИКИ
1) 
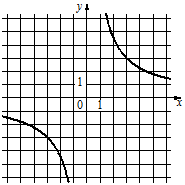2) 
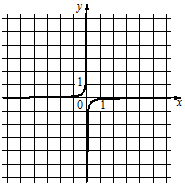3) 
В таблице под каждой буквой укажите соответствующий номер.
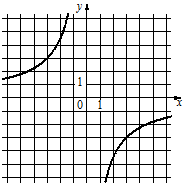
Рассмотрим графики. Все они являются гиперболами.
Рассмотрим функции. Они тоже все являются гиперболическими.
Заметим, что на графиках 2) и 3) гиперболы располагаются во II и IV четвертях, а парабола графика 1) располагается в I и III четвертях.
Что это означает...
Для графика 1) когда "х" положителен, то и "у" положителен, а когда "х" отрицателен, то и "у" отрицателен.
Под такие условия подходит только формула Б).
С остальными графиками все просто:
К примеру, возьмем x=3 и посмотри на графики:
Для графика 3) "y" будет равен -3, что соответствует формуле А) (y=-9/x=-9/3=-3).
Для графика 2) "y" будет довольно маленьким, что очень похоже на формулу В) y=-1/(9x)=-1/(9*3)=-1/27.
Ответ:
| А) | Б) | В) |
| 3) | 1) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)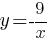
Б)
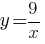В)
ГРАФИКИ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры в первой половине суток. Ответ дайте в градусах Цельсия.
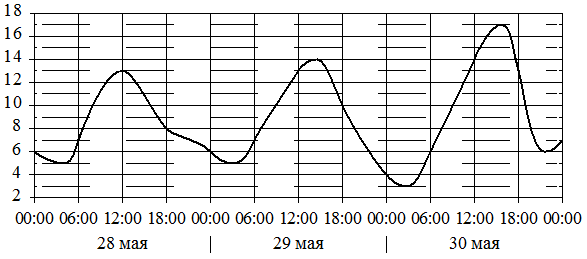На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 30 мая. Ответ дайте в градусах Цельсия.
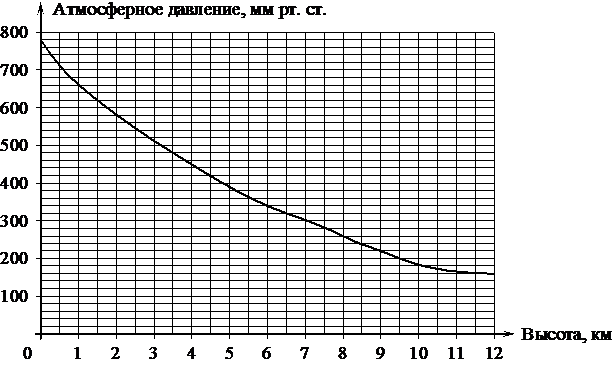На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 1 км. Ответ дайте в миллиметрах ртутного столба.
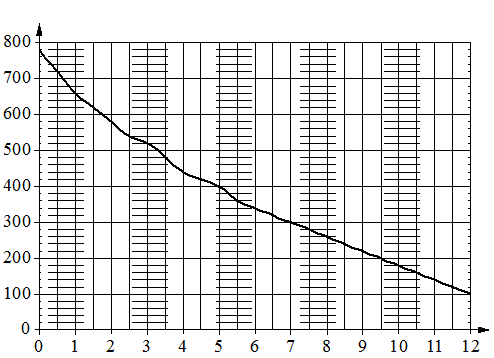На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 620 миллиметрам ртутного столба. Ответ дайте в километрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: