
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 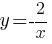 Б)
Б) 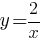 В)
В) 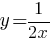
ГРАФИКИ
1) 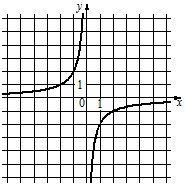 2)
2)  3)
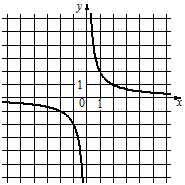
3) 
В таблице под каждой буквой укажите соответствующий номер.
Рассмотрим графики. Все они являются гиперболами.
Рассмотрим функции. Они тоже все являются гиперболическими.
Заметим, что на графиках 2) и 3) гиперболы располагаются во I и III четвертях, а парабола графика 1) располагается в II и IV четвертях.
Что это означает...
Для графика 1) когда "х" положителен, то "у" отрицателен, а когда "х" отрицателен, то "у" положителен.
Под такие условия подходит только формула А).
С остальными графиками все просто:
К примеру, возьмем x=2 и посмотри на графики:
Для графика 3) "y" будет равен 2, что соответствует формуле Б) (y=2/x=2/2=1).
Для графика 2) "y" будет довольно маленьким, что очень похоже на формулу В) y=1/(2x)=1/(2*2)=1/4=0,25.
Ответ:
| А) | Б) | В) |
| 1) | 3) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
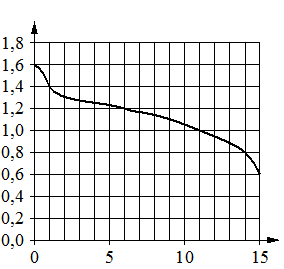 При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1 В.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1 В.
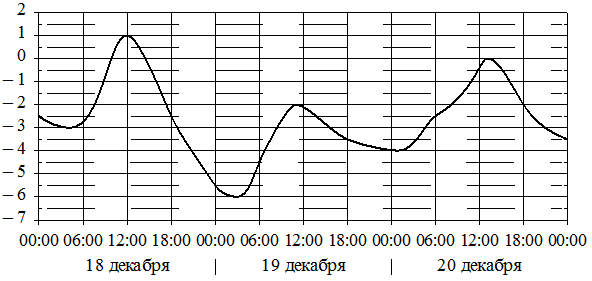 На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 19 декабря. Ответ дайте в градусах Цельсия.
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 19 декабря. Ответ дайте в градусах Цельсия.
Постройте график функции 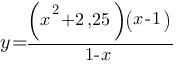 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции 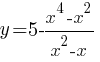 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии: