Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
x*x+x-6x, при x≥0
(-x)x+(-x)-6x, при x<0
x2-5x, при x≥0
-x2-7x, при x<0
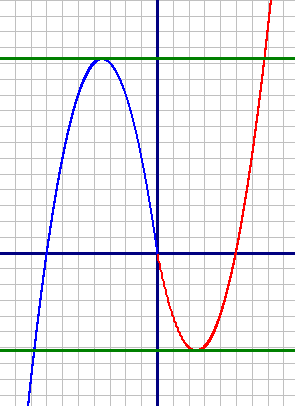Обе подфункции - параболы. Построим их по точкам:
y1=x2-5x (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -4 | -6 | -6 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 6 | 10 | 12 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=x2-5|x|+4. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
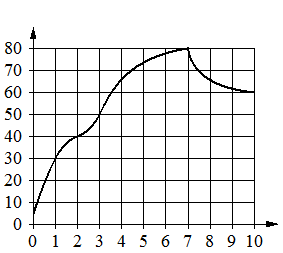На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
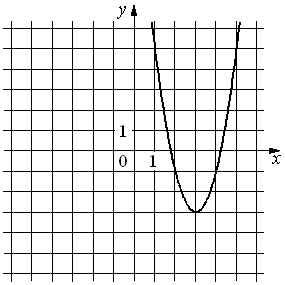На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [0; 2] 2) [2; 5] 3) [4; 7] 4) [1; 7] |
Установите соответствие между графиками функций и формулами, которые их задают.
| ФУНКЦИИ | ГРАФИКИ | ||
|
1) y=-(2/x) 2) y=x2-2 3) y=2x 4) y=2/x |
А)  |
Б)  |
В)  |
Известно, что графики функций y=x2+p и y=-2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-10-11 11:33:07) Администратор: Зызын, а где вы взяли это равенство?
(2021-04-05 14:46:10) Зызын: а как так получилось , что -x = 4x(x + 4)?
(2017-04-26 18:54:00) Администратор: Алмо, Вы понимаете как получилось (-x)x+(-x)-6x? А дальше все просто: (-x)x+(-x)-6x=-x^2-x-6x=-x^2-7x
(2017-04-26 09:10:39) Алмо: Почему при раскрытии модуля получается -х²-7х?
(2015-05-17 23:34:41) Администратор: Алена, сначала определить координаты вершины, а потом заполнять таблицу для построения, конечно, удобней, но не обязательно.
(2015-05-16 20:22:31) Алена: Почему не определяются координаты вершин (по формулам xB=-b2a,уВ=подставляем полученное значение хВ), когда мы заполняем таблицу для построения? Это делать не обязательно?
(2015-05-16 19:58:41) Алена: Почему не определяются координаты вершин (по формулам xB=-b2a,уВ=подставляем полученное значение хВ), когда мы заполняем таблицу для построения? Это делать не обязательно?
(2015-05-16 19:57:49) Алена: Почему не определяются координаты вершин (по формулам xB=-b2a,уВ=подставляем полученное значение хВ), когда мы заполняем таблицу для построения? Это делать не обязательно?