
Известно, что графики функций y=x2+p и y=-2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Чтобы найти общую точку двух графиков, надо найти решение системы, составленное из уравнений этих графиков:
 y=x2+p
y=x2+p
y=-2x-2
x2+p=-2x-2
x2+2x+p+2=0
Это квадратное уравнение должно иметь только один корень, т.к. по условию, графики пересекаются только в одной точке. Следовательно, дискриминант должен быть равен нулю.
D=22-4*1*(p+2)=4-4p-8=-4-4p=0
p=-1
Получаем уравнение:
x2+2x-1+2=0
x2+2x+1=0
(x+1)2=0
x=-1 - это координата х точки пересечения.
y=-2x-2=-2*(-1)-2=0 - это координата y точки пересечения.
Получаем: координаты точки пересечения графиков (-1;0).
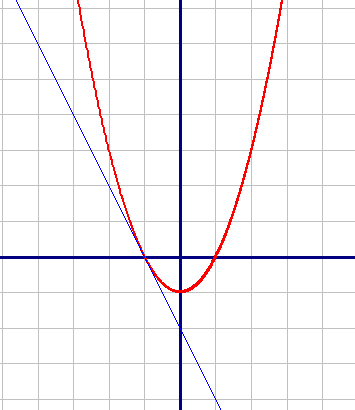 Построим графики по точкам:
Построим графики по точкам:
y=x2+p=x2-1 (Красный график)
| X | -2 | -1 | 0 | 1 | 2 |
| Y | 3 | 0 | -1 | 0 | 3 |
| X | -2 | -1 | 0 |
| Y | 2 | 0 | -2 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=4|x-3|-x2+8x-15 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k>0, b<0 Б) k>0, b>0 В) k<0, b>0 |
1)  |
2)  |
3)  |
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A) 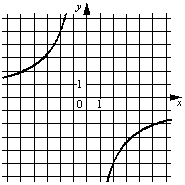 Б)
Б) 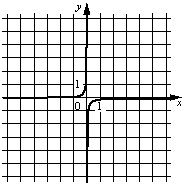 В)
В) 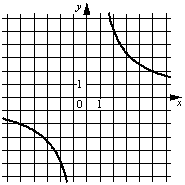
ФОРМУЛЫ
1) y=-10/x
2) y=-1/(10x)
3) y=10/x
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции y=2x+6|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции
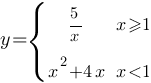 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Комментарии: