Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A)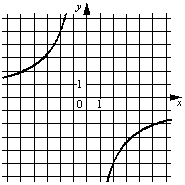 
Б) 
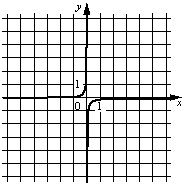В)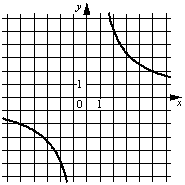 
ФОРМУЛЫ
1) y=-10/x
2) y=-1/(10x)
3) y=10/x
В таблице под каждой буквой укажите соответствующий номер.
Рассмотрим графики. Все они являются гиперболами.
Рассмотрим функции. Они тоже все являются гиперболическими.
Заметим, что на графиках А) и Б) гиперболы располагаются во II и IV четвертях, а парабола графика В) располагается в I и III четвертях.
Это означает, что для графика В) когда "х" положителен, то и "у" положителен, а когда "х" отрицателен, то и "у" отрицателен.
Под такие условия подходит только формула 3).
Далее все просто:
Возьмем x=2 и посмотри на графики:
Для графика А) "y" будет равен -5, что соответствует формуле 1).
Для графика Б) "y" будет довольно маленьким, что очень похоже на формулу 2) y=-1/(10x)=-1/(10*2)=-1/20=-0,05.
Ответ: А) - 1), Б) - 2), В) - 3).
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции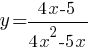 
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
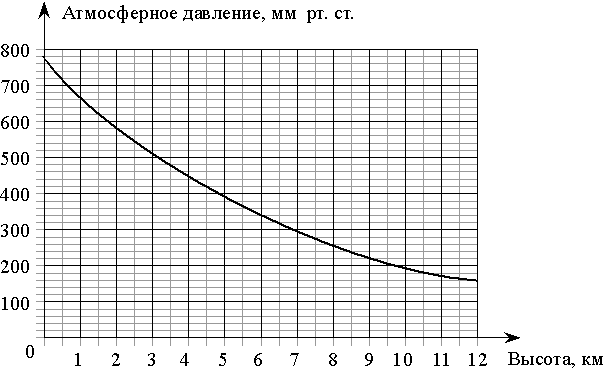На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
Постройте график функции y=x2+14x-3|x+8|+48 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
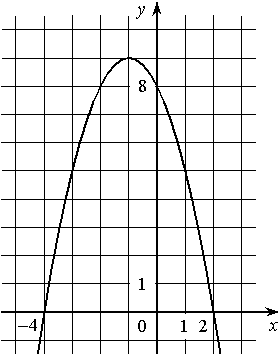На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
Постройте график функции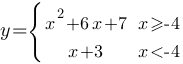 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: