Постройте график функции y=x2-5|x|+4. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
В данной функции присутствует
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x2-5x+4, при x≥0
y=x2-5(-x)+4, при x<0
y=x2-5x+4, при x≥0
y=x2+5x+4, при x<0
Рассмотрим и построим график для каждой подфункции на определенном им диапазонах и объединим их.
График обеих подфункций - парабола, при чем, ветви параболы направлены вверх (так как коэффициент "а" больше нуля).
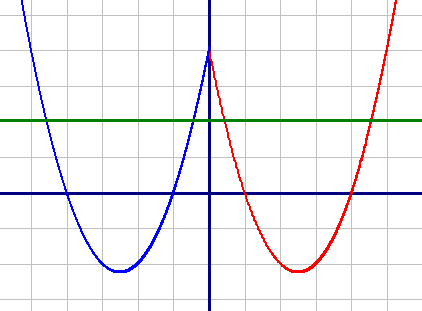Для первой подфункции (красная):
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 4 | 0 | -2 | -2 | 0 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 4 | 0 | -2 | -2 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 
при x=√32, y=1/8.
Постройте график функции 
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Какое из данных ниже чисел является значением выражения 
1) 35/11
2) 1/14
3) 5/7
4) 5/77
Найдите значение выражения (√125+√5)*√5.
Решите уравнение x3+5x2=9x+45.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: