
Постройте график функции y=|x|(x-1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
 x(x-1)-6x, при x≥0
x(x-1)-6x, при x≥0
-x(x-1)-6x, при x<0
 x2-x-6x, при x≥0
x2-x-6x, при x≥0
-x2+x-6x, при x<0
 x2-7x, при x≥0
x2-7x, при x≥0
-x2-5x, при x<0
Рассмотрим каждую подфункцию:
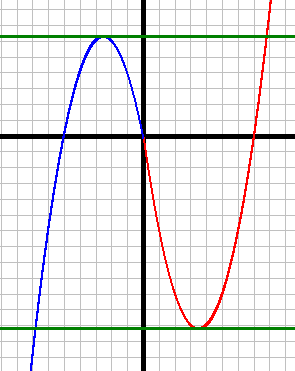 1) y=x2-7x, при x≥0 (красный график)
1) y=x2-7x, при x≥0 (красный график)
Найдем корни уравнения x2-7x=0, чтобы узнать, в каких точках график пересекает ось х.
x2-7x=0
x(x-7)=0
x1=0
x2=7
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -6 | -10 | -12 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 4 | 6 | 6 |
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение (x2-36)2+(x2+4x-12)2=0.
Какое из данных ниже чисел является значением выражения 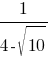 ?
?
1) 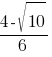
2) 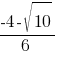
3) 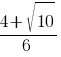
4) 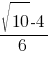
При смешивании первого раствора кислоты, концентрация которого 30%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 45% кислоты. В каком отношении были взяты первый и второй растворы?
Найдите значение выражения 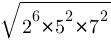
1) 78400
2) 70
3) 280
4) √
Найдите значение выражения 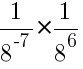
Комментарии: