
Постройте график функции y=4|x-3|-x2+8x-15 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
|x-3|=x-3, при x-3≥0 (т.е. x≥3)
|x-3|=-(x-3), при х-3<0 (т.е. х<3)
Тогда вся функция будет выглядеть так:
 4(x-3)-x2+8x-15, при x≥3
4(x-3)-x2+8x-15, при x≥3
-4(x-3)-x2+8x-15, при x<3
 4x-12-x2+8x-15, при x≥3
4x-12-x2+8x-15, при x≥3
-4x+12-x2+8x-15, при x<3
 -x2+12x-27, при x≥3
-x2+12x-27, при x≥3
-x2+4x-3, при x<3
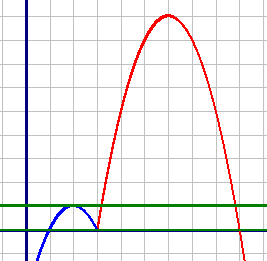 График обеих подфункций - парабола, у обеих подфункций коэффициент "а" равен -1, т.е. меньше нуля. Следовательно, ветви обеих парабол направлены вниз.
График обеих подфункций - парабола, у обеих подфункций коэффициент "а" равен -1, т.е. меньше нуля. Следовательно, ветви обеих парабол направлены вниз.
Построим по точкам графики обеих подфункций, но первый график на диапазоне от 3 до +∞, а второй график на диапазоне от -∞ до 3 (как указано в системе).
Подункция y=-x2+12x-27 (Красный график)
| X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 0 | 5 | 8 | 9 | 8 | 5 | 0 |
| X | 3 | 2 | 1 |
| Y | 0 | 1 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
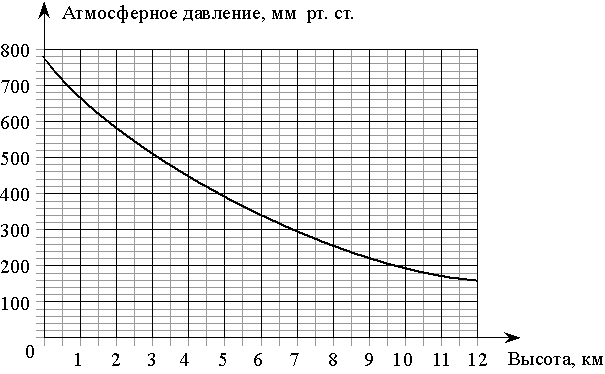 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 360 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 360 миллиметров ртутного столба?
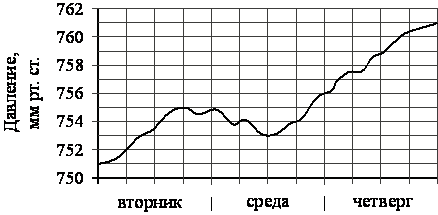 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Постройте график функции 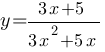 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФУНКЦИИ | ГРАФИКИ | ||
|
1) y=-(2/x) 2) y=x2-2 3) y=2x 4) y=2/x |
А)  |
Б)  |
В)  |
Комментарии: