
Постройте график функции y=5|x-3|-x2+7x-12 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствует модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
|x-3|=x-3, при x-3≥0 (т.е. x≥3)
|x-3|=-(x-3), при х-3<0 (т.е. х<3)
Тогда вся функция будет выглядеть так:
 5(x-3)-x2+7x-12, при x≥3
5(x-3)-x2+7x-12, при x≥3
-5(x-3)-x2+7x-12, при x<3
 5x-15-x2+7x-12, при x≥3
5x-15-x2+7x-12, при x≥3
-5x+15-x2+7x-12, при x<3
 -x2+12x-27, при x≥3
-x2+12x-27, при x≥3
-x2+2x+3, при x<3
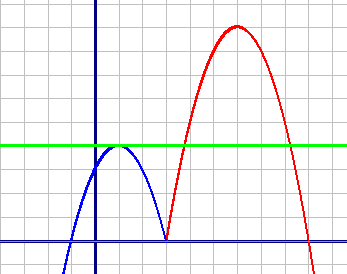 Построим по точкам графики обеих функций, но первый график на диапазоне от 3 до +∞, а второй график на диапазоне от -∞ до 3 (как указано в системе).
Построим по точкам графики обеих функций, но первый график на диапазоне от 3 до +∞, а второй график на диапазоне от -∞ до 3 (как указано в системе).
Функция y=-x2+12x-27 (Красный график)
| X | 3 | 5 | 7 | 9 |
| Y | 0 | 8 | 8 | 0 |
| X | 3 | 2 | 1 | 0 | -1 |
| Y | 0 | 3 | 4 | 3 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
Квадратный трёхчлен разложен на множители: x2+2x-35=(x-5)(x-a). Найдите a.
Сократите дробь 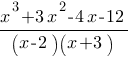
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s=nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l=60 см, n=1900? Ответ выразите в километрах.
Решите уравнение (x-2)(x-3)(x-4)=(x-3)(x-4)(x-5).
Найдите значение выражения 61a-11b+50, если (2a-7b+5)/(7a-2b+5)=9.
Комментарии: