Решите уравнение (4x-8)2(x-8)=(4x-8)(x-8)2.
(4x-8)2(x-8)=(4x-8)(x-8)2
(4x-8)2(x-8)-(4x-8)(x-8)2=0
Вынесем за общую скобку (4x-8)(x-8):
(4x-8)(x-8)((4x-8)-(x-8))=0
(4x-8)(x-8)(4x-8-x+8)=0
(4x-8)(x-8)3x=0 |:3
(4x-8)(x-8)x=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим 3 варианта:
1) 4x-8=0 => x1=2
2) x-8=0 => x2=8
3) x3=0
Ответ: x1=2, x2=8, x3=0
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 
1) -1/8
2) -8
3) 8
4) 1/8
Найдите значение выражения 
при x=-13.
Решите систему уравнений 
Найдите значение выражения (2-c)2-c(c+4) при c=-1/8.
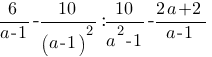
Постройте график функции 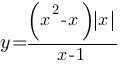y=|x|(x-1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: