
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=2/x 2) y=x2-2 3) y=2x 4) y=2-x2 |
А)  |
Б)  |
В)  |
Рассмотрим формулы.
1) y=2/x - гипербола
2) y=x2-2 - парабола
3) y=2x - прямая
4) y=2-x2 - парабола
Рассмотрим графики.
А) - Прямая
Б) - Гипербола
В) - Парабола
Сопоставить однозначно можно графики прямой и гиперболы:
А) - 3), Б) - 1)
Ветви параболы, на графике В) смотрят вниз, следовательно в формуле коэффициент "а" должен быть отрицательным. Подходит только формула 4).
Ответ: А) - 3), Б) - 1), В) - 4)
Поделитесь решением
Присоединяйтесь к нам...
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=4x имеет с графиком ровно одну общую точку.
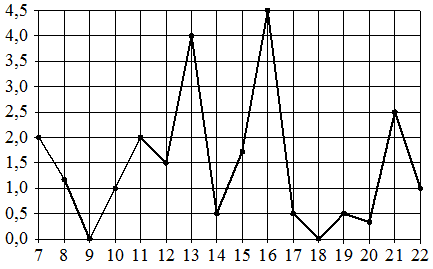 На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки
на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Мурманске в данный период. Ответ дайте в миллиметрах.
На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки
на рисунке соединены линией. Определите по рисунку, какое наибольшее суточное количество осадков выпадало в Мурманске в данный период. Ответ дайте в миллиметрах.
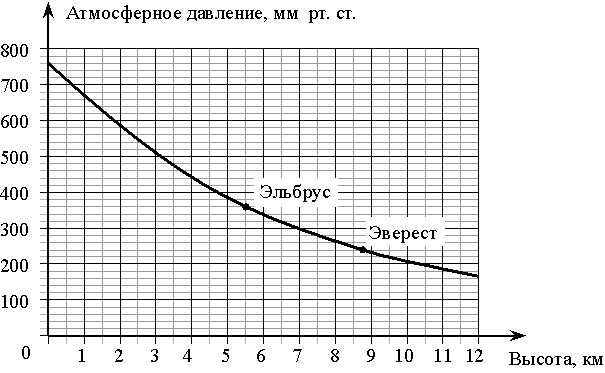 На графике изображена зависимость атмосферного давления от высоты местности над уровнем моря. По горизонтали указана высота над уровнем моря в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
На графике изображена зависимость атмосферного давления от высоты местности над уровнем моря. По горизонтали указана высота над уровнем моря в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
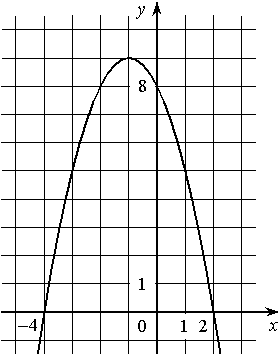 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Функция убывает на промежутке [-1;+∞)
2) ƒ(0)>ƒ(1)
3) Наибольшее значение функции равно 8
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) k>0, b>0 2) k<0, b>0 3) k>0, b<0 4) k<0, b<0 |
А)  |
Б)  |
В)  |
Комментарии: