
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
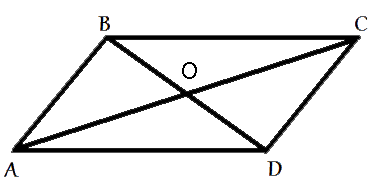 Рассмотрим треугольники ABC и ACD.
Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников, AB=CD и BC=AD (по
свойству параллелограмма), следовательно рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACD, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок DO - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь COD равна половине площади треугольника ACD. SCOD=SACD/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
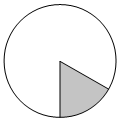 Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
 В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
 Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
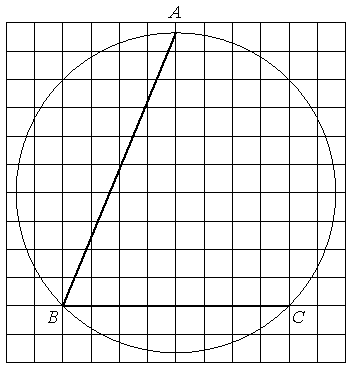 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
Комментарии: