Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-3 2) y=x-3 3) y=-3x 4) y=3x |
А)  |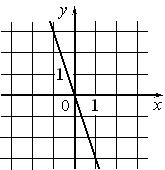
Б)  |
В)  |
Рассмотрим каждый график:
| А)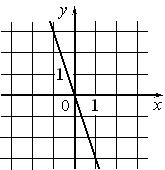
| Прямая проходит под наклоном через начало координат. Следовательно, этому графику соответствует или функция y=-3x, или функция y=3x. Так как прямая проходит через 2-ую и 4-ую четверти системы координат, то коэффициент при X отрицательный, т.е. данному графику соответствует функция y=-3x. |
| Б) |
Данная прямая рассекает 1-ую и 3-ю четверти, следовательно коэффициент при X положительный. Прямая не проходит через начало координат, следовательно свободный коэффициент не равен нулю. Подходит только функция y=x-3. |
| В) |
Данная прямая параллельна оси x, следовательно коэффициент при X равен нулю. Подходит только функция y=-3. |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
y=x|x|-|x|-2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-x2+2x+5
Б) y=x2+2x-5
В) y=-x2-2x+5
ГРАФИКИ
1) 
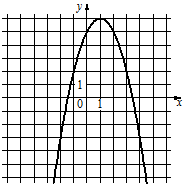2) 
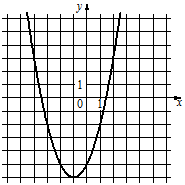3) 
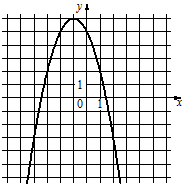
В таблице под каждой буквой укажите соответствующий номер.
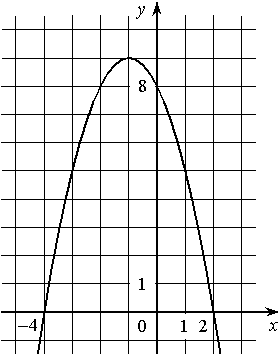На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
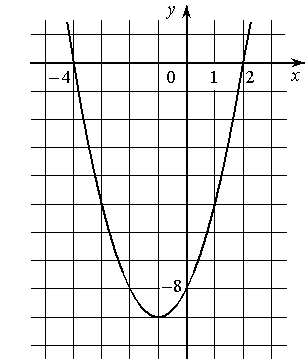На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) Наименьшее значение функции равно -8
2) f(-4)>f(1)
3) f(x)<0 при -4<x<2
Постройте график функции y=x2-|6x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: