
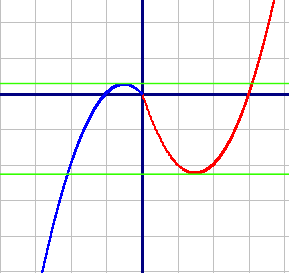
Постройте график функции
y=x|x|-|x|-2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
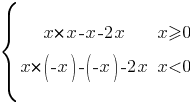
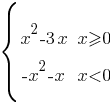
 Обе подфункции - параболы. Построим их по точкам:
Обе подфункции - параболы. Построим их по точкам:
y1=x2-3x на диапазоне от 0 до плюс бесконечности (красный график):
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | -2 | -3 | 0 | 4 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 0 | -2 | -6 |
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 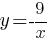 Б)
Б) 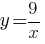 В)
В) 
ГРАФИКИ
1) 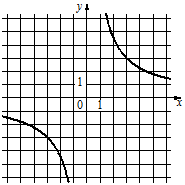 2)
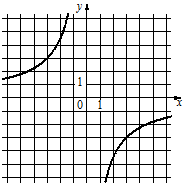
2) 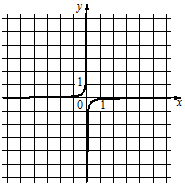 3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
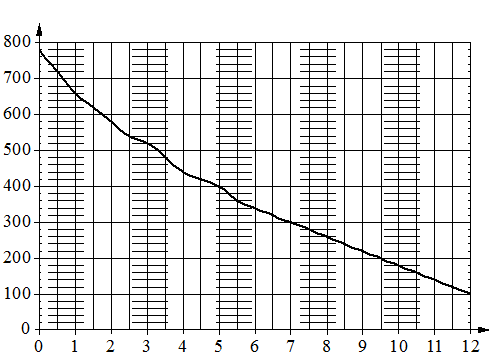 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 11 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 11 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=-x2-0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
| А) | 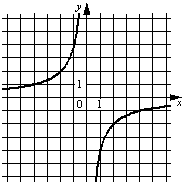 |
Б) | 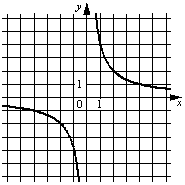 |
В) |  |
ФОРМУЛЫ 1) y=-1/4x 2) y=4/x 3) y=-4/x 4) y=1/4x |
Комментарии: