Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=-x2-0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=-x2-0,25
y=kx
kx=-x2-0,25
x2+kx+0,25=0
Найдем корни
этого уравнения:
D=k2-4*1*0,25=k2-1
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=k2-1=0
k2=1
k1=1
k2=-1
Получаем функции:
y=-x2-0,25
y=x
y=-x
построим графики:
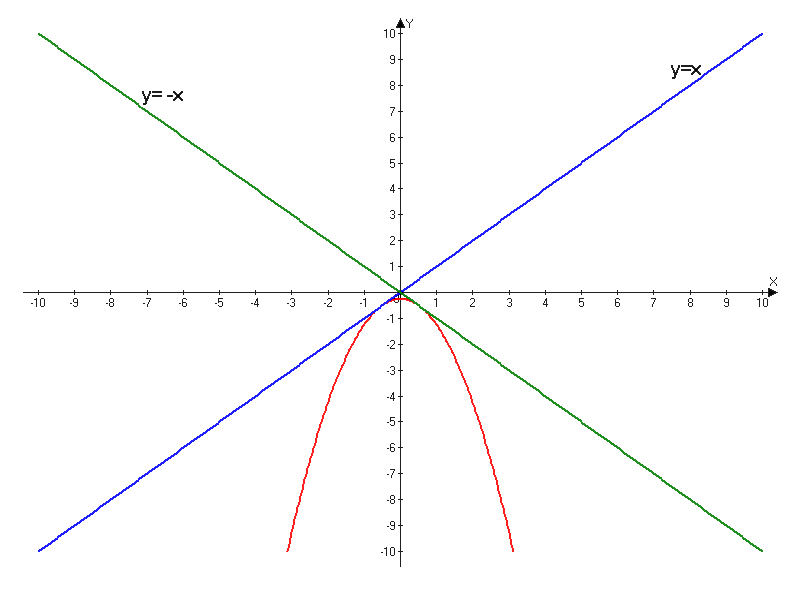
Поделитесь решением
Присоединяйтесь к нам...
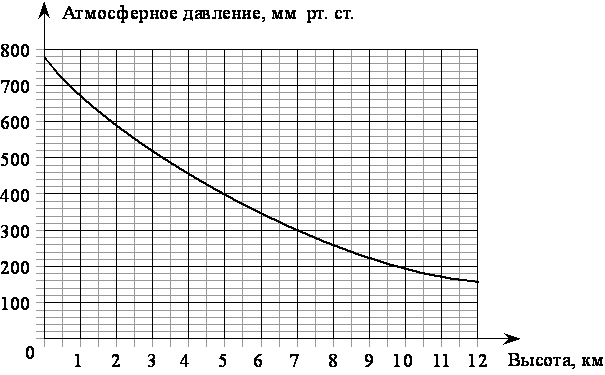На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 1 км. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции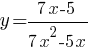 
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Постройте график функции y=x2-|6x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции y=4|x+6|-x2-11x-30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
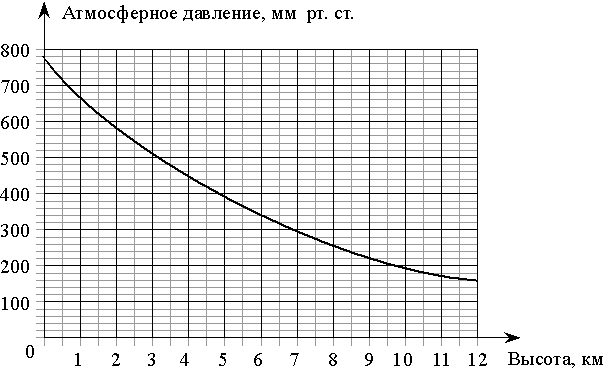На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: