
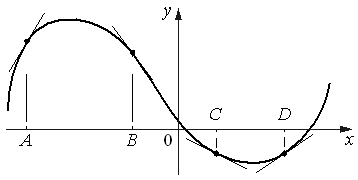
 На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A |
1) 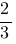
|
| B |
2) 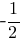
|
| C |
3) 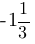
|
| D |
4) 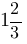
|
Производную от функции, в данном случае, лучше рассматривать как тангенс угла наклона касательной.
Если тангенс положительный (т.е. угол острый), то и производная положительна и наоборот.
Тогда сразу можно сказать, что в точках A и D - значение производной положительно.
А в точках B и C - отрицательно.
Если посмотреть на таблицу углов, то ставится понятно, что при увеличени угла значение тангенса увеличивается (tg0°=0, tg45°=1, tg90°=+∞).
Следовательно, значение тангенса в точке A больше значения тангенса в точке D.
Получаем, что:
В точке A - значение производной равно 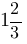 .
.
В точке D - значение производной равно 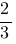 .
.
При дальнейшем увеличении угла (от 90° до 180°) значение тангенса меняется от -∞ до 0, т.е. уменьшается.
Следовательно, в точке B значение производной равно 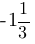 , а в точке C - значение производной равно
, а в точке C - значение производной равно 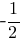 .
.
Ответ:
| A | B | C | D |
| 4) | 3) | 2) | 1) |
Поделитесь решением
Присоединяйтесь к нам...
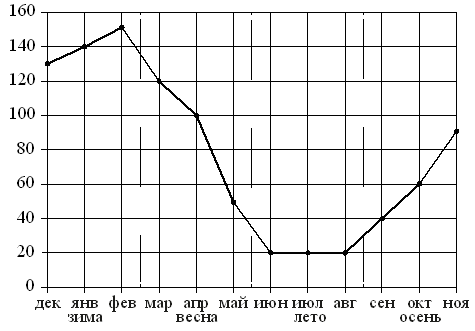 На рисунке точками показаны объёмы месячных продаж обогревателей
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.
На рисунке точками показаны объёмы месячных продаж обогревателей
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) зима | 1) ежемесячный объём продаж рос, но был меньше 100 штук |
| Б) весна | 2) ежемесячный объём продаж падал |
| В) лето | 3) ежемесячный объём продаж рос и был больше 120 штук |
| Г) осень | 4) ежемесячный объём продаж не менялся в течение всего периода |
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ФУНКЦИИ
А) 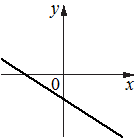 Б)
Б) 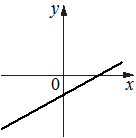 В)
В) 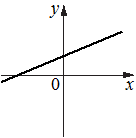 Г)
Г) 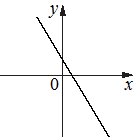
КОЭФФИЦИЕНТЫ
1) k<0, b<0
2) k>0, b>0
3) k>0, b<0
4) k<0, b>0
В таблице под каждой буквой укажите соответствующий номер.
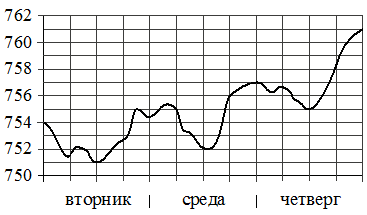 На рисунке изображён график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.
На рисунке изображён график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.
Определите по рисунку наименьшее значение атмосферного давления
за данные три дня (в миллиметрах ртутного столба).
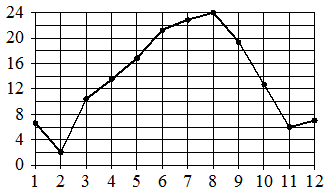 На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указаны номера месяцев,
по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией.
На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указаны номера месяцев,
по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией.
Определите по рисунку, в каком месяце среднемесячная температура в Сочи была наименьшей за данный период. В ответе укажите номер этого месяца.
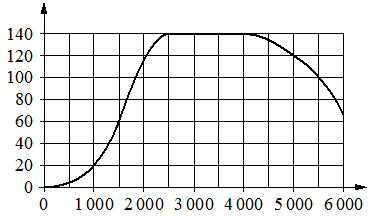 На графике показана зависимость крутящего момента автомобильного двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н?м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 20 Н*м.
На графике показана зависимость крутящего момента автомобильного двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н?м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 20 Н*м.
Определите по графику, какого наименьшего числа оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение.
Комментарии: