Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 140 литров она заполняет на 3 минуты дольше, чем вторая труба?
v - скорость, с которой первая труба пропускает воду
v+6 - скорость, с которой вторая труба пропускает воду
t - время заполнения резервуара первой трубой
t-3 - время заполнения резервуара второй трубой
Получаем систему:
vt=140
(v+6)(t-3)=140
vt=(v+6)(t-3)
vt=vt-3v+6t-18
0=-3v+6t-18
18+3v=6t |:3
6+v=2t
t=(6+v)/2
Подставляем это значение в первое уравнение:
v(6+v)/2=140
v(6+v)=280
6v+v2=280
v2+6v-280=0
Решим это
квадратное уравнение через
дискриминант:
D=62-4*1*(-280)=36+1120=1156
v1=(-6+34)/(2*1)=28/2=14
v2=(-6-34)/(2*1)=-40/2=-20
Так как скорость не может быть отрицательной, то подходит только 14.
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
О числах a и c известно, что a<c. Какое из следующих неравенств неверно
1) a+8<c+8
2) -a/33<-c/33
3) a-2<c-2
4) -a/33<c/33
Укажите решение неравенства 4x-4≥9x+6.
1) [-0,4;+∞)
2) (-∞;-2]
3) [-2;+∞)
4) (-∞;-0,4]
На каком рисунке изображено множество решений системы неравенств
x<3,
4-x>0?
1) 
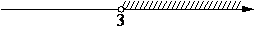
2) 
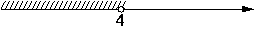
3) 
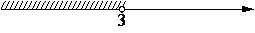
4) 
Решите систему неравенств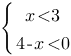 
На каком рисунке изображено множество её решений?
1) 
2) Система не имеет решений
3) 
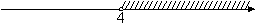
4) 
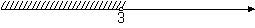
Решите систему неравенств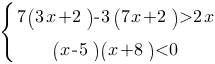 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: