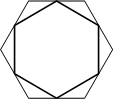
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
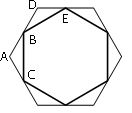Рассмотрим треугольники ABC и BDE. Т.к. стороны
правильного шестиугольника равны, то и CA=AB=BD=DE, /A=/D, т.к. углы
правильного шестиугольника тоже равны. Следовательно, данные треугольники равны (по первому
признаку равенства треугольников). Тогда BC=BE.
Углы /BCA=/CBA=/EBD=/BED (по свойству
равнобедренного треугольника). Следовательно внутренние углы /С=/B=/E.
Данные выкладки справедливы для любой пары треугольников,следовательно все стороны внутреннего шестиугольника равны и все внутренние углы равны. Это означает, что внутренний шестиугольник - правильный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
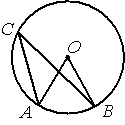Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: