
 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
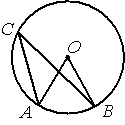
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию ∠AOB=84°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 84°.
∠ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Соответственно, 84/2=42.
Ответ: 42
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
 Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
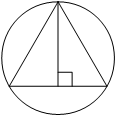
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
Комментарии: