
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
Рассмотрим треугольник ABD.
BO перпендикулярен AD (по условию задачи), т.е. ∠BOD=∠BOA=90°.
∠ABO=∠DBO (т.к. BE -
биссектриса).
Получается, что треугольники ABO и DBO равны (по
второму признаку равенства треугольников).
Следовательно, AB=BD.
Т.е. треугольник ABD -
равнобедренный.
BO -
биссектриса этого треугольника, следовательно и
медиана, и
высота (по третьему
свойству равнобедренного треугольника).
Следовательно, AO=OD=AD/2=192/2=96.
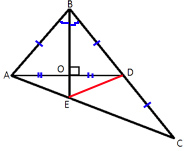 Проведем отрезок ED и рассмотрим треугольник BEC.
Проведем отрезок ED и рассмотрим треугольник BEC.
ED -
медиана этого треугольника, так как делит сторону BC пополам.
Площади треугольников EDC и EDB равны (по второму
свойству медианы). SEDC=SEDB=(BE*OD)/2=(192*96)/2=96*96=9216
SABE=(BE*AO)/2=(192*96)/2=9216
Т.е.
SABE=SEDC=SEDB=9216
Тогда, SABС=3*9216=27648
AD -
медиана треугольника ABC (по условию), следовательно делит треугольник на два равных по площади треугольника ABD и ACD (по
второму свойству медианы).
SABD=(AD*BO)/2=SABC/2
(192*BO)/2=27648/2
BO=27648/192=144
Рассмотрим треугольник ABO, он
прямоугольный, тогда применим
теорему Пифагора:
AB2=BO2+AO2
AB2=1442+962
AB2=20736+9216=29952
AB=√
BC=2AB=2*48√
Рассмотрим треугольник AOE.
OE=BE-BO=192-144=48
Так как этот треугольник тоже
прямоугольный, то можно применить
теорему Пифагора:
AE2=AO2+OE2
AE2=962+482=9216+2304=11520
AE=√
Так как BE -
биссектриса, то используя ее
первое свойство запишем:
BC/AB=CE/AE
96√
2=CE/(48√
CE=96√
AC=AE+CE=48√
Ответ: AB=48√
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
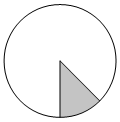 Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Комментарии: