Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
Рассмотрим треугольники BMP и CPM:
MP - общая сторона
BP=PC (по условию задачи)
/BPM=/CPM, т.к. /BPM - прямой, а /CPM - ему
смежный.
Следовательно треугольники BMP и CPM равны (по
первому признаку). Отсюда следует, что BM=MC=MA.
Рассмотрим треугольник BMC. Т.к. MB=MC, то этот треугольник
равнобедренный, следовательно /MCP=/PBM (по
свойству равнобедренных треугольников).
В треугольнике ABM аналогичная ситуация, /BAM=/ABM.
Т.е. получается, что /BAM+/MCP=/ABC. Из
теоремы о сумме углов треугольника следует, 180°=/BAM+/MCP+/ABC
180°=/ABC+/ABC
180°=2*/ABC
90°=/ABC
Из чего следует, что треугольник ABC -
прямоугольный. По
свойству описанной окружности следует, что точка М - центр окружности, следовательно AC - диаметр => AC=2*R=2*7=14.
Ответ: AC=14.
Поделитесь решением
Присоединяйтесь к нам...
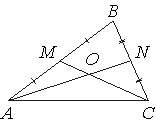Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 21°?
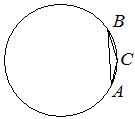В треугольнике ABC угол C равен 150°, AB=4. Найдите радиус окружности, описанной около этого треугольника.
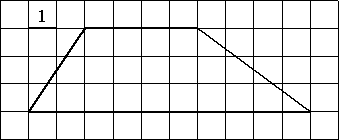Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: