
 Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Рассмотрим треугольники ABC и ABH.
∠A - общий
∠AHB=∠ABC
Следовательно, эти треугольники
подобны (по
признаку подобия)
Тогда AC/AB=AB/AH (гипотенуза большого треугольника относится к гипотенузе маленького как малый катет большого треугольника к малому катету маленького треугольника)
45/AB=AB/5
45*5=AB2
225=AB2
AB=15
Ответ: AB=15
Поделитесь решением
Присоединяйтесь к нам...
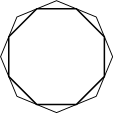 Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
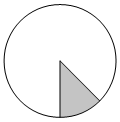 Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
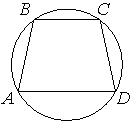 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
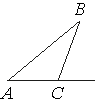 В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
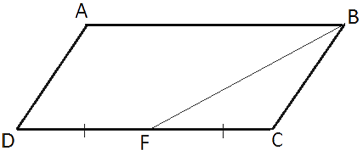 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Комментарии: