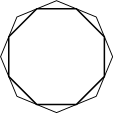
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
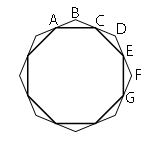Так как углы меньшего многоугольника располагаются на середине сторон, а сторон восемь, значит и углов будет восемь. Т.е. меньший многоугольник является восьмиугольником. Теперь докажем, что он правильный.
Рассмотрим треугольники ABC, CDE и EFG. AB=BC=CD=DE=EF=FG (по
определению правильного многоугольника).
/ABC=/CDE=/EFG (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=...и так далее
В итоге, по
определению правильного многоугольника получается, меньший восьмиугольник - правильный.
Поделитесь решением
Присоединяйтесь к нам...
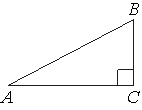В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
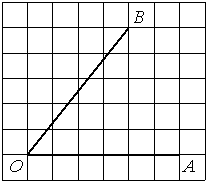Найдите тангенс угла AOB, изображённого
на рисунке.
Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
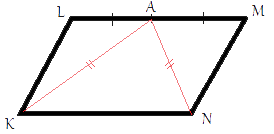В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: