
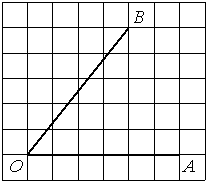
 Найдите тангенс угла AOB, изображённого
на рисунке.
Найдите тангенс угла AOB, изображённого
на рисунке.
Проведем высоту из точки В к отрезку OA, чтобы получился
прямоугольный треугольник:
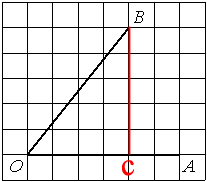 Получился треугольник OBC с катетами ОС (длина 4) и BC (длина 5).
Получился треугольник OBC с катетами ОС (длина 4) и BC (длина 5).
По определению тангенса:
tgAOB=BC/OC=5/4=1,25
Ответ: 1,25
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
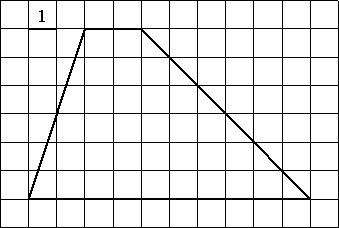 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
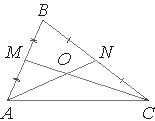 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
 В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
Комментарии: