
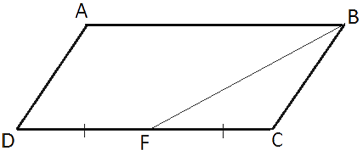 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
BC=CD/2=CF (по условию задачи)
Следовательно треугольник BCF -
равнобедренный.
По
свойству равнобедренного треугольника:
∠CFB=∠CBF
∠CFB=∠ABF (так как это
накрест-лежащие углы)
Получается, что ∠CBF=∠ABF
Следовательно, BF -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
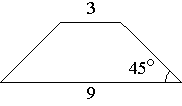 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
 Медиана равностороннего треугольника равна 9√
Медиана равностороннего треугольника равна 9√
Комментарии:
(2022-09-12 10:35:22) : АВ = CD = 14 см, ВС = AD = 27 см за властивостями параллелограмма Р ABCD = АВ + CD + ВС + AD Р ABCD = … Відповідь :