
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Рассмотрим треугольники ABC и MBN.
/B - общий.
/BAC=/BMN (т.к. это
соответственные углы)
/BCA=/BNM (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
AC/MN=BC/BN
AC/MN=BC/(BC-NC)
42/12=BC/(BC-25)
7/2=BC/(BC-25)
7(BC-25)=2BC
7BC-175=2BC
5BC=175
BC=35
BN=BC-NC=35-25=10
Ответ: BN=10
Поделитесь решением
Присоединяйтесь к нам...
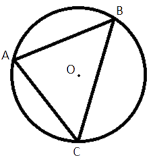 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
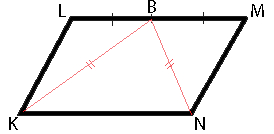 В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
 Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
Комментарии: