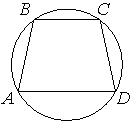
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Рассмотрим основания трапеции, как параллельные прямые (они параллельны по
определению трапеции), а сторону AB как секущую.
Тогда углы A и B - это односторонние. Сумма таких углов равна 180°.
∠A+∠B=180°
∠B=180°-∠A=180°-31°=149°
Ответ: 149
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
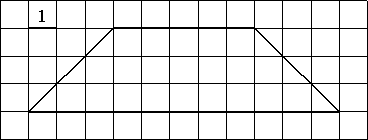Найдите площадь трапеции, изображённой на рисунке.
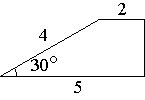Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: