
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
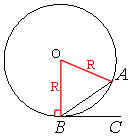 Проведем радиусы к точкам A и B, как показано на рисунке.
Проведем радиусы к точкам A и B, как показано на рисунке.
∠AOB - центральный и опирается на дугу в 26°, следовательно:
∠AOB=26°
Треугольник AOB - равнобедренный, так как две его стороны - это радиусы окружности.
Тогда, по свойству равнобедренного треугольника, углы при основании равны, обозначим их α.
По
теореме о сумме углов треугольника:
∠AOB+∠OAB+∠OBA=180°
26°+α+α=180°
2α=180°-26°=154°
α=154°/2=77°
По
свойству касательной ∠OBC=90°.
∠ABC=∠OBC-∠OBA
∠ABC=90°-77°=13°
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
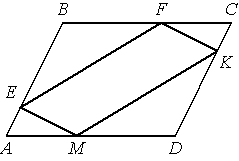 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
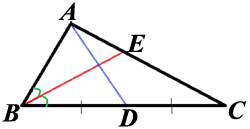 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Комментарии: