
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ550 –Η–Ζ 1087 |
 –ù–Α–Ι–¥–Η―²–Β –±–Ψ–Κ–Ψ–≤―É―é ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η ―É–≥–Μ―΄ ABC –Η BCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 60¬Α –Η 135¬Α, –Α CD=36.
–ù–Α–Ι–¥–Η―²–Β –±–Ψ–Κ–Ψ–≤―É―é ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η ―É–≥–Μ―΄ ABC –Η BCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 60¬Α –Η 135¬Α, –Α CD=36.
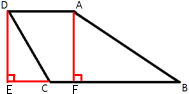 –î–Ψ―΅–Β―Ä―²–Η–Φ –Ψ―²―Ä–Β–Ζ–Κ–Η –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–î–Ψ―΅–Β―Ä―²–Η–Φ –Ψ―²―Ä–Β–Ζ–Κ–Η –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
DE=AF, ―².–Κ. ―ç―²–Ψ
–≤―΄―¹–Ψ―²―΄
―²―Ä–Α–Ω–Β―Ü–Η–Η.
∠DCE=180¬Α-∠BCD=180¬Α-135¬Α=45¬Α (―².–Κ. ―ç―²–Ψ
―¹–Φ–Β–Ε–Ϋ―΄–Β ―É–≥–Μ―΄).
sin(∠DCE)=ED/CD (–Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é)
sin45¬Α=ED/CD (sin45¬Α=√
√
ED=36√
sin(∠ABF)=AF/AB (–Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é)
sin60¬Α=ED/AB
AB=ED/sin60¬Α (sin60¬Α=√
AB=(18√
–û―²–≤–Β―²: AB=12√
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ü–Β―Ä–Η–Φ–Β―²―Ä –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Β–Ϋ 184. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Κ–≤–Α–¥―Ä–Α―²–Α.
–ü–Β―Ä–Η–Φ–Β―²―Ä –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Β–Ϋ 184. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Κ–≤–Α–¥―Ä–Α―²–Α.
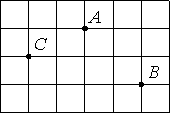 –ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A, B –Η C. –ü–Μ–Ψ―â–Α–¥―¨ –Ψ–¥–Ϋ–Ψ–Ι –Κ–Μ–Β―²–Κ–Η ―Ä–Α–≤–Ϋ–Α 1. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η A –¥–Ψ ―¹–Β―Ä–Β–¥–Η–Ϋ―΄ –Ψ―²―Ä–Β–Ζ–Κ–Α BC.
–ù–Α –Κ–Μ–Β―²―΅–Α―²–Ψ–Ι –±―É–Φ–Α–≥–Β –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A, B –Η C. –ü–Μ–Ψ―â–Α–¥―¨ –Ψ–¥–Ϋ–Ψ–Ι –Κ–Μ–Β―²–Κ–Η ―Ä–Α–≤–Ϋ–Α 1. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η A –¥–Ψ ―¹–Β―Ä–Β–¥–Η–Ϋ―΄ –Ψ―²―Ä–Β–Ζ–Κ–Α BC.
–ß–Β―Ä–Β–Ζ ―¹–Β―Ä–Β–¥–Η–Ϋ―É K –Φ–Β–¥–Η–Α–Ϋ―΄ BM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Η –≤–Β―Ä―à–Η–Ϋ―É A –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –Ω―Ä―è–Φ–Α―è, –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―â–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ―É BC –≤ ―²–Ψ―΅–Κ–Β P. –ù–Α–Ι–¥–Η―²–Β –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –Κ –Ω–Μ–Ψ―â–Α–¥–Η ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α KPCM.
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―Ä–Α–≤–Ϋ―΄ 13 –Η 11, –Α ―¹―Ä–Β–¥–Ϋ―è―è –Μ–Η–Ϋ–Η―è ―Ä–Α–≤–Ϋ–Α 10.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η, –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―Ä–Α–≤–Ϋ―΄ 13 –Η 11, –Α ―¹―Ä–Β–¥–Ϋ―è―è –Μ–Η–Ϋ–Η―è ―Ä–Α–≤–Ϋ–Α 10.
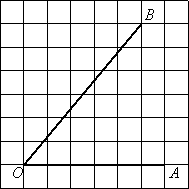 –ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α AOB.
–ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α AOB.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: